ELECTRON - HIGGS FIELD INTERACTION
Everything that we can touch and see and feel has substance. All this substance that makes up our Universe is courtesy of the familiar atom, which gives us all the matter around us. An atom is comprised of lightweight electrons orbiting and bound to a bulky nucleus of protons and neutrons, which themselves are made of quarks.
Our Universe with massless electrons
The electron is extremely light, with a mass just over 0.0000000000000000000000000009 grams (or about 0.51 MeV/c2). We believe that it gains this (albeit tiny) mass due to the fact that it is influenced by the Higgs field. Without this influence, our Universe would have a completely different structure.In a simple hydrogen atom for example, the radius of the electron's orbit is inversely proportional to the electron’s mass. A massless electron would therefore be at infinity from the proton, not allowing atoms to form at all.
Protons, neutrons and the Higgs boson
In Nature, heavier particles tend to decay into lighter, more stables particles. Spontaneous radioactive β decay occurs when neutrons inside the nucleus are converted into protons, by the emission of a W− particle — a heavy particle that also gets its mass due to the Higgs field.In addition, the up and down quarks, that combine to form protons (uud) as well as neutrons (udd), gain mass from their interaction with the Higgs field. However, their masses contribute only ~1% of the mass of protons and neutrons. The bulk of the mass comes from the energy holding the quarks together, which is greater for the proton than the neutron.
Without the Higgs field, quarks would have no mass and consequently the proton would be heavier than the neutron, since all their mass would come from their respective binding energies. Now, without the Higgs field, the W− particle would have a much smaller mass, protons would spontaneously and almost instantly decay into neutrons — we would have a Universe without protons.
Our familiar Universe with galaxies, supernovae, planets and life would not exist without mass, and our very existence is thanks to the all-pervading Higgs field.

Image by rawpixel on freepik.com
Acquiring Of Mass By Electron
the stronger a particle directly interacts with the Higgs field, the larger its mass will be. Fundamentally, a particle mass is a measure of its direct interaction with the Higgs field. This way, we can also relate particles' speeds to their masses. The larger a particle mass is, the slower it will be, due to its 'friction' with the Higgs field. Photons, which do not interact directly with the Higgs field, and thus massless, are the fastest.
So, some elementary particles are massive due to their direct interactions with the ubiquitous Higgs field which is almost homogeneous and constant all over the space. For example, an electron acquires its mass due to its direct interaction with the Higgs field in a definite strength. Another particle has a larger/smaller mass than the electron's because it has a stronger/weaker interaction with the Higgs field than the electron's.
Electron on the scale
A measurement of electron mass which is more precise by a factor of 13 could have an impact on the fundamental laws of physicsElectrons are the quantum glue of our world. Without electrons there would be no chemistry, and light would be unable to interact with matter. If electrons were only a little heavier or lighter than they are, the world would look radically different. But how can a particle which is so tiny that it has so far been considered point-like actually be weighed? This feat has now been achieved in a collaborative project involving physicists from the Max Planck Institute for Nuclear Physics in Heidelberg who "weighed" the mass of the electron 13 times more precisely than previously known. As electron mass is involved in fundamental physical constants, it is of significance to fundamental physics.
This research in precision physics to improve a fundamental value by a single order of magnitude has attacted a huge response that this result is of a great significance at scientific conferences. In just a few years, scientists have managed to determine the value for the mass of an electron more precisely by a factor of 13. This experiment needes the extremely high sensitivity of the "scale" used to achieve this result.
The fact that physicists now know the mass of the electron to eleven decimal places is important, because electrons are pretty much ubiquitous. Just reading this text means that electrons must convert light into nerve impulses in the eyes. These minuscule particles, which, according to current knowledge, have no spatial extent, thus have immense power in nature. Their mass is linked to, among other things, the value of fundamental physical constants. One example is the "fine-structure constant" which determines the shape and properties of atoms and molecules. It basically describes everything we can see because it plays a central role in the interaction between light and matter. If nature had given electrons an only slightly different mass, atoms would look completely different. Such a world would probably be very strange.
Electron mass is measured together with a carbon nucleus
The mass of the electron is also a central variable in the so-called standard model of physics, which describes three of the four currently known fundamental forces of physics. Although the model works impressively well, it is now nevertheless clear that there are limits to its validity. Where the limits of the standard model lie however, is an open question. Precise knowledge of the mass of the electron can thus be of vital assistance in the search for previously unknown physical interrelationships.Physicists developed an ingenious experiment in order to determine the electron's extremely small mass. Weighing, in principle, requires a reference for comparison. If you get on the scales in the morning, in old mechanical models it is a spring. Beam scales have a counterweight as reference. In the case of the electron, the physicists faced the problem that all fundamental particles, which could meaningfully be used as reference weights, are much heavier. The proton or neutron, for example, is two thousand times heavier which would be like trying to weigh a rabbit with an elephant as the counterweight. So for their experiment, the physicists made use of a cunning strategy. Although they brought two vastly unequal masses together, they didn’t even try to weigh the electron rabbit directly with the help of an atomic elephant.
The experiment was set up so that tThe main challenge was to develop the measurement method to carry out the precise measurement of the electron mass. The physicists paired a single electron with a bare nucleus of the immensely heavier carbon (C) 12 isotope. This carbon isotope was chosen with careful consideration, as it is the basis for the atomic mass unit. The mass of C 12 is by definition exactly known and using it as a reference excludes a major source of error. Controlling systematic error is absolutely vital in this experiment.
Penning trap sets the carbon ion racing around a circuit
The physicists blasted off five of the carbon atom's six electrons in order to prepare a C12 nucleus with a single electron. The remaining carbon ion with a charge of five - the carbon nucleus with a single electron - was set racing around a circuit which, viewed in a highly simplified way, can be thought of as circular. A so-called Penning trap with its extremely uniform magnetic field forces the carbon ion to follow this circular path.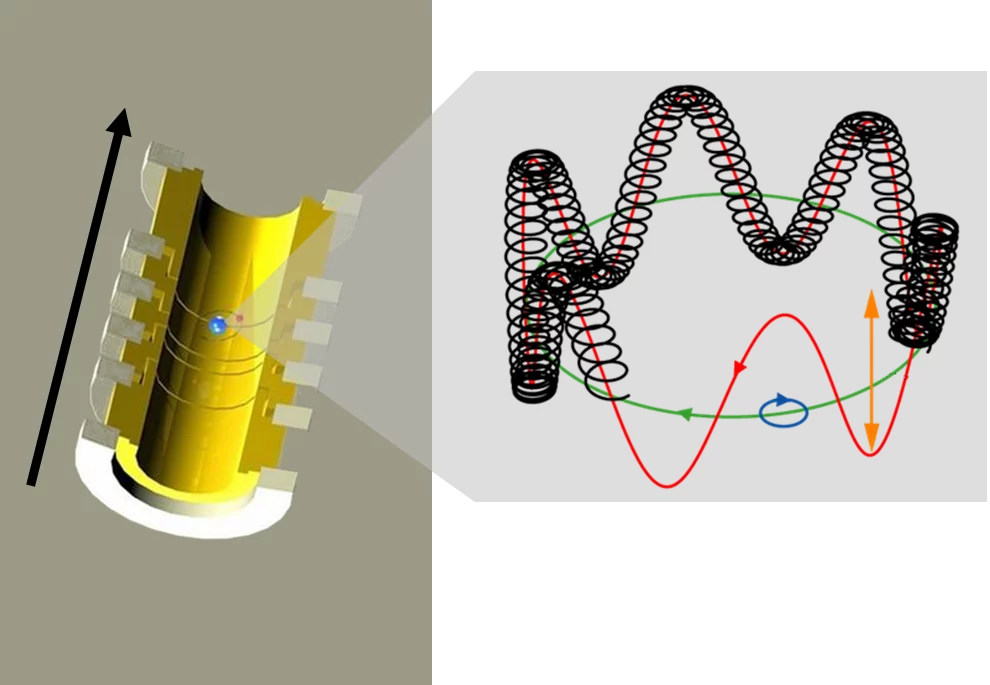
The aim, when making precision measurements, is always to make the measured variable precisely countable. the thinking behind the method is : In a Formula 1 race on a circuit, spectators can count how many times a racing car shoots past and, if they know the length of the circuit, can estimate the car's speed. The situation is similar in a Penning trap; however in this case, the physicists were able to measure even the tiniest fractions of complete circuits.
Quantum mechanics was of assistance in the second step, which was then required for determining the mass of the electron. Electrons have what is known as "spin" that makes them act like tiny magnets. In the strong magnetic field of a Penning trap, this spin precesses or wobbles like a tiny gyroscope. Although this precession is extremely rapid, the physicists had a strategy to measure it precisely. The key is that the revolution frequency of the carbon ion in the trap and the wobble frequency of electron precession are in an exact ratio to one another. Like a gear mechanism, quantum mechanics links the mass of the carbon ion firmly to the mass of the electron, which is thereby measurable.
Only a theoretical contribution enabled the measurement of the electron mass
There was, however, a rather poorly understood "gearwheel" in the mechanism known as the g factor or gyromagnetic factor. On the basis of previous results , they were able to calculate the g factor more precisely than in the past, thus enabling an exact determination of the electron mass.Scientists made significant contributions collaboratively to perform such a high-precision experiment. The result is a fantastically precise number revealing that an electron has a mass 1/1836.15267377 that of a proton. Stated in kilograms, the electron's mass is around an unimaginable 10-30 kilogram, or thirty zeros after the decimal point. Although the electron truly is a lightweight, it plays a heavyweight role in nature.
