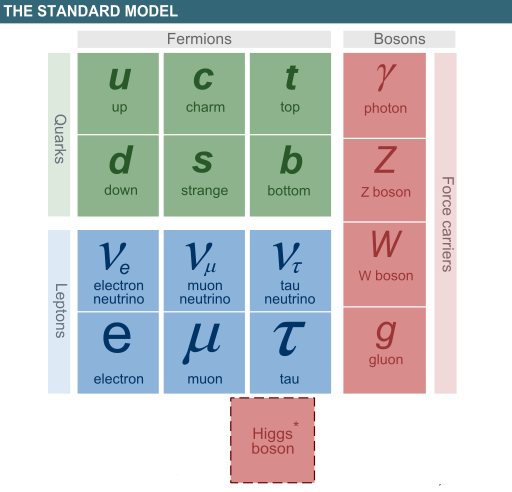
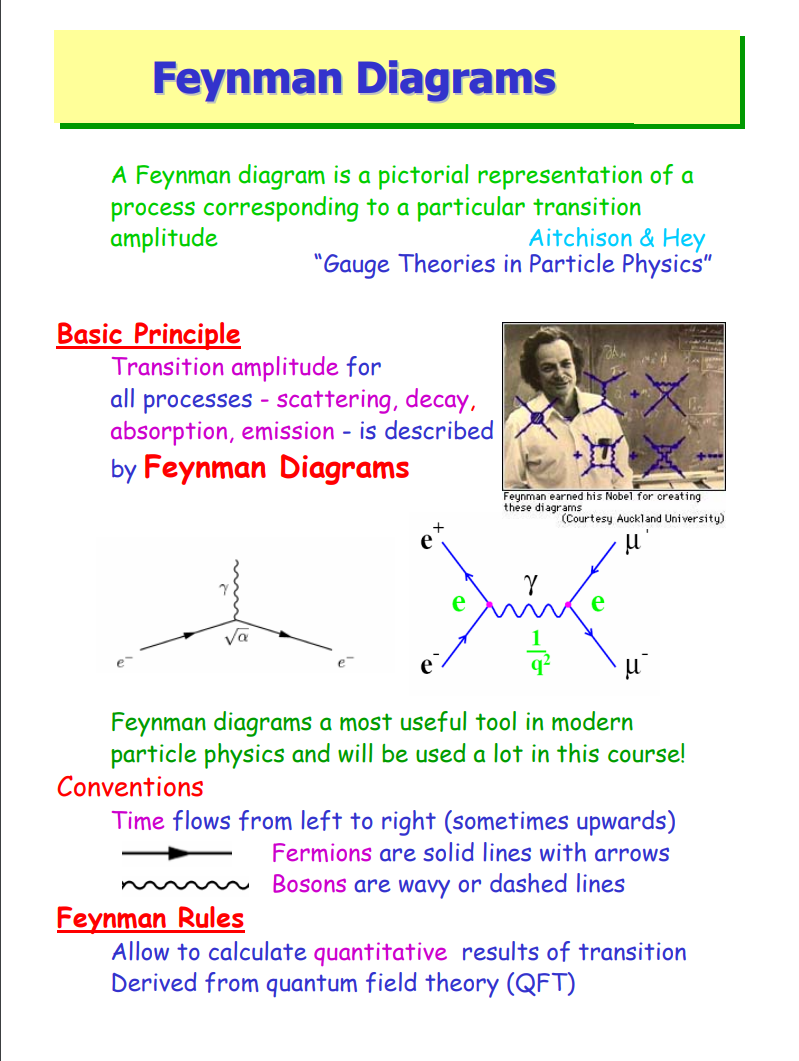
Quantum electrodynamics (QED), quantum field theory of the interactions of charged particles with the electromagnetic field. It describes mathematically not only all interactions of light with matter but also those of charged particles with one another. QED is a relativistic theory in that Albert Einstein’s theory of special relativity is built into each of its equations. Because the behaviour of atoms and molecules is primarily electromagnetic in nature, all of atomic physics can be considered a test laboratory for the theory. Some of the most precise tests of QED have been experiments dealing with the properties of subatomic particles known as muons. The magnetic moment of this type of particle has been shown to agree with the theory to nine significant digits. Agreement of such high accuracy makes QED one of the most successful physical theories so far devised.
QED rests on the idea that charged particles (e.g., electrons and positrons) interact by emitting and absorbing photons, the particles that transmit electromagnetic forces. These photons are “virtual”; that is, they cannot be seen or detected in any way because their existence violates the conservation of energy and momentum. The photon exchange is merely the “force” of the interaction, because interacting particles change their speed and direction of travel as they release or absorb the energy of a photon. Photons also can be emitted in a free state, in which case they may be observed as light or other forms of electromagnetic radiation.