Nuclear Physics - Deducing The Mass Formula Of The Nucleus
There is more complexity to the mass formula of the nucleus than just a simple linear dependence on the total number of nucleons which are protons and neutrons. Let us call it \(A\) . Readily at first , there seems to be the kinds of energies mentioned below that should play the key role:
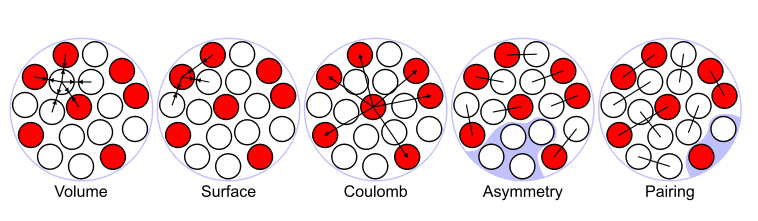
- Bulk energy: This is the term studied above, and saturation implies that the energy is proportional to \(B_{\text{bulk}}=\alpha A\).
- Surface energy: Nucleons at the surface of the nuclear sphere have less neighbors, and should feel less attraction. Since the surface area goes with \(R^2\), we find \(B_{\text{surface}}=-\beta A\).
- Pauli or symmetry energy: nucleons are fermions (will be discussed later). That means that they cannot occupy the same states, thus reducing the binding. This is found to be proportional to \(B_{\text{symm}}=-\gamma (N/2-Z/2)^2/A^2\).
- Coulomb energy: protons are charges and they repel. The average distance between is related to the radius of the nucleus, the number of interaction is roughly \(Z^2\) (or \(Z(Z-1)\)). We have to include the term \(B_{\text{Coul}}=-\epsilon Z^2/A\).
Taking all this together we fit the formula
\[B(A,Z) = \alpha A - \beta A^{2/3} - \gamma (A/2-Z)^2A^{-1} - \epsilon Z^2 A^{-1/3} \label{eq:mass1}\]
to all know nuclear binding energies with \(A\geq 16\) (the formula is not so good for light nuclei). The fit results are given in Table \(\PageIndex{1}\).
| parameter | value |
|---|---|
| \(\alpha\) | 15.36 MeV |
| \(\beta\) | 16.32 MeV |
| \(\gamma\) | 90.45 MeV |
| \(\epsilon\) | 0.6928 MeV |
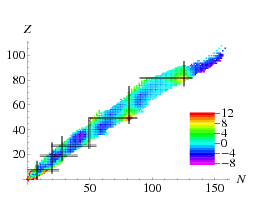
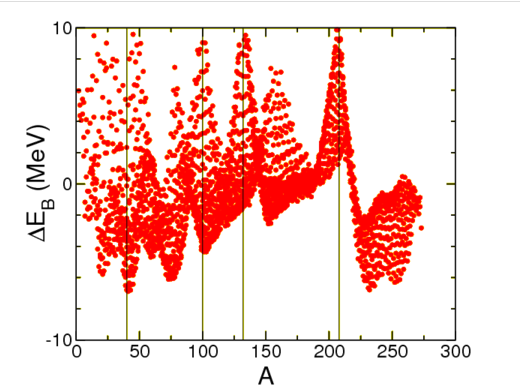
In Table \(\PageIndex{1}\) we show how well this fit works. There remains a certain amount of structure, see below, as well as a strong difference between neighbouring nuclei. This is due to the superfluid nature of nuclear material: nucleons of opposite momenta tend to anti-align their spins, thus gaining energy. The solution is to add a pairing term to the binding energy,
\[B_{\text{pair}} = \begin{cases} A^{-1/2} & \text{for $N$ odd, $Z$ odd}\\ - A^{-1/2} & \text{for $N$ even, $Z$ even}\end{cases}\]
The results including this term are significantly better, even though all other parameters remain at the same position (Table \(\PageIndex{2}\)). Taking all this together we fit the formula
\[B(A,Z) = \alpha A - \beta A^{2/3} - \gamma (A/2-Z)^2A^{-1} - \delta B_{\text{pair}}(A,Z)-\epsilon Z^2 A^{-1/3} \label{eq:mass2}\]
| parameter | value |
|---|---|
| \(\alpha\) | 15.36 MeV |
| \(\beta\) | 16.32 MeV |
| \(\gamma\) | 90.46 MeV |
| \(\delta\) | 11.32 MeV |
| \(\epsilon\) | 0.6929 MeV |