Nuclear Physics - Deeper Analysis Of The Nuclear Masses
- Each nucleus has a (positive) charge \(Ze\), and integer number times the elementary charge \(e\). This follows from the fact that atoms are neutral!
- Nuclei of identical charge come in different masses, all approximate multiples of the “nucleon mass”. (Nucleon is the generic term for a neutron or proton, which have almost the same mass, \(m_p= 938.272 \text{MeV}/c^2\), \(m_n= \text{MeV}/c^2\).) Masses can easily be determined by analysing nuclei in a mass spectrograph which can be used to determine the relation between the charge \(Z\) (the number of protons, we believe) vs. the mass.
Nuclei of identical charge (chemical type) but different mass are called isotopes. Nuclei of approximately the same mass, but different chemical type, are called isobars.
We conclude that the nucleus of mass \(m\approx A m_N\) contains \(Z\) positively charged nucleons (protons) and \(N=A-Z\) neutral nucleons (neutrons). These particles are bound together by the “nuclear force”, which changes the mass below that of free particles. We shall typically write \(^{A}\)El for an element of chemical type El, which determines \(Z\), containing \(A\) nucleons.
To analyze the masses even better we use the atomic mass unit (amu), which is 1/12th of the mass of the neutral carbon atom,
\[1 \text{ amu} = \frac{1}{12} m_{^{12}\mathrm{C}}.\]
This can easily be converted to SI units by some chemistry. One mole of \(^{12}\)C weighs \(0.012\text{ kg}\), and contains Avogadro’s number particles, thus
\[1 \text{ amu} = \frac{0.001}{N_A} \text{ kg} = 1.66054 \times 10^{-27} \text{ kg} = 931.494 \text{MeV}/c^2.\]
The quantity of most interest in understanding the mass is the binding energy, defined for a neutral atom as the difference between the mass of a nucleus and the mass of its constituents,
\[B(A,Z) = Z M_H c^2 + (A-Z) M_n c^2 - M(A,Z)c^2.\]
With this choice a system is bound when \(B>0\), when the mass of the nucleus is lower than the mass of its constituents. Let us first look at this quantity per nucleon as a function of \(A\), see Figure \(\PageIndex{1}\).
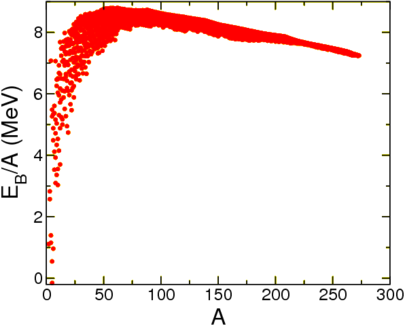
This seems to show that to a reasonable degree of approximation the mass is a function of \(A\) alone, and furthermore, that it approaches a constant. This is called nuclear saturation. This agrees with experiment, which suggests that the radius of a nucleus scales with the 1/3rd power of \(A\),
\[R_{\text{RMS}}\approx 1.1 A^{1/3} \text{ fm}.\]
This is consistent with the saturation hypothesis made by Gamov in the 30’s:
saturation hypothesis
As \(A\) increases the volume per nucleon remains constant.
For a spherical nucleus of radius \(R\) we get the condition
\[\frac{4}{3}\pi R^3 = A V_1,\]
or
\[R = \left(\frac{V_13}{4\pi}\right)^{1/3} A^{1/3}.\]
From which we conclude that
\[V_1 = 5.5 \text{ fm}^3\]
