COHERENCE AND QUANTUMNESS ARE IMPORTANT THEORETICAL FACTORS
Extended considerations of the quantum nature of energy transmission and its significance, such as for the reliability or effectiveness of photosynthetic processes, can be found in recent research. It is becoming more and more usual to compare coherence to "nontrivial" quantum effects. Coherence is a well-known characteristic of classical systems as well, such as the oscillation of a pendulum or the propagation of electromagnetic waves (28, 29), in which a clearly defined phase connection is maintained. Coherence is not, however, exclusively a trait of quantum systems. Because coherence does not automatically imply quantumness, it is important to define it while discussing "quantum coherent energy transport."
However, it can be challenging to determine precisely what underlying physical events are being described because the definition of coherence is sometimes kept vague. To make things more understandable, we offer a functional definition of coherence in the context of the ultrafast spectroscopic observables as detailed in the following.
It is interesting to note that fundamental questions about how to handle the thermal equilibration of a quantum subsystem coupled to an environment (see below) as well as the relationships and subtle differences between coherences, "correlations," and "intermolecular couplings" also arose in great detail in the development of nuclear magnetic resonance a few decades ago, while considering coherent superpositions of spins on molecules separated by micrometres. Additionally, it had been made clear that a traditional bath does not result in an adequate thermalization at low temperatures.

Coherence is the technical word for off-diagonal elements in any density matrix. However, we believe that this general definition is too wide to be useful because the physical significance of these off-diagonal matrix elements fully depends on the basis used (for example, site or excitonic basis). Thus, in this context, we favour a more limited vocabulary that generally corresponds to the widespread usage in contemporary work on ultrafast spectroscopy.
The communication barriers between the experimental and theoretical communities serve as a good example of this issue with term definition. In particular, we refer to the problems originating from the introduction of coherence as off-diagonal elements of the density matrix on the basis of localised pigment states. In theoretical simulations, these coherences "appear" as oscillations in the site basis (fig. S5 illustrates an example of heavily damped oscillations in site basis coherences), but the physical meaning is simply that the excitations in the system are somewhat spatially delocalized.
When considering spatial correlations and levels of localization of the excitons, this information is helpful. However, whenever it is possible to selectively photoexcite single pigments in a linked system, there are only time-dependent (oscillatory) spectroscopic signals associated with these coherences. The essential linear superposition of system eigenstates can be produced (for a small number of systems) by carefully adjusting the laser pulse amplitude and phase, although this method is obviously limited to highly specialised laboratory settings.
The off-diagonal elements in the density matrix that forms the basis of a system's eigenstates are what we believe to be a more practical definition of coherence and the one that is most closely related to the meaning of the term in recent experimental literature (i.e., corresponding to the excitonic basis in the absence of vibronic mixing). The degree to which the (light-induced) state of the molecular system corresponds to a linear superposition of various eigenstates (for example, excitons) of the system is quantified by the physical interpretation of these elements. These superpositions are nonstationary and evolve over time as damped oscillations with a frequency that corresponds to the energy difference between the involved eigenstates when generated by brief laser pulses.
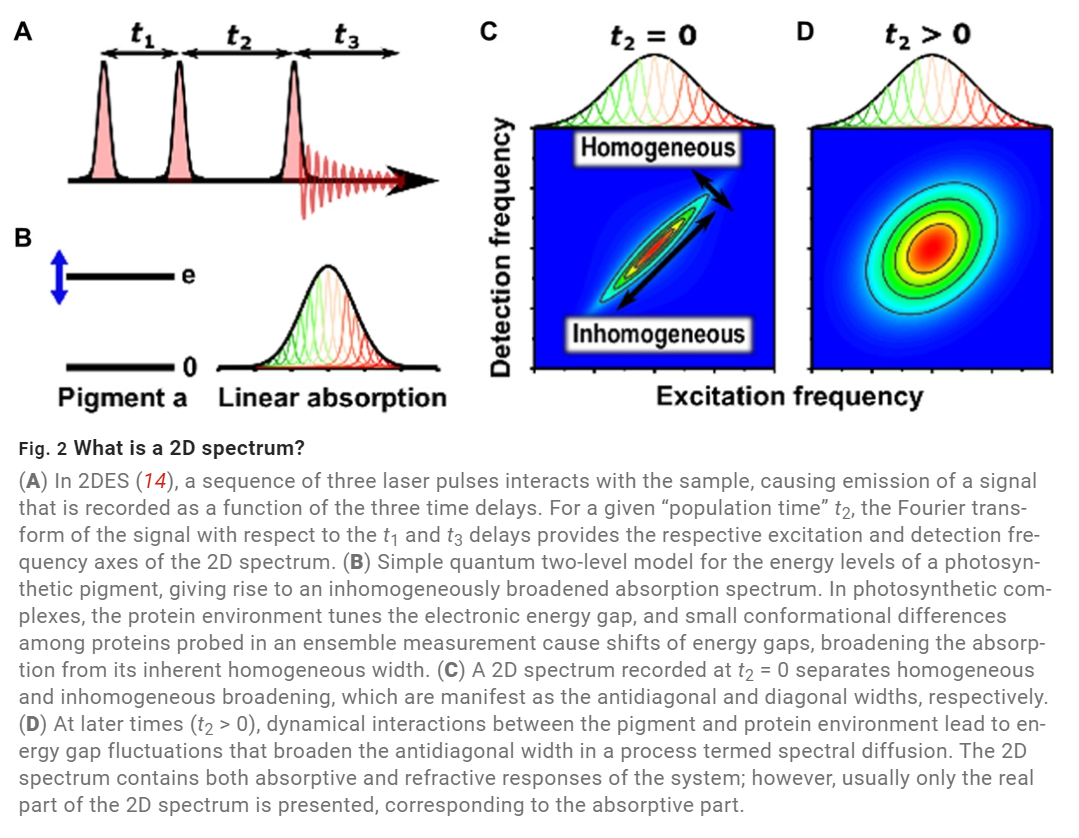
It is important to draw still another distinction in the context of dynamics: Optical coherences are the formal name for the particular superposition of ground and excited states. The transition frequencies and homogenous linewidth of the absorption spectrum are determined by the evolution of optical coherence. It arises in optical 2D studies at coherence times t1 and t3 (see Figs. 2 and 3 for details). However, energy transfer, which is a significant concept in the site basis, is not directly related to optical coherence, which gives information on the system-bath interactions relevant to electronic decoherence. However, as our analytical estimate below will demonstrate, the two are also not entirely unconnected.
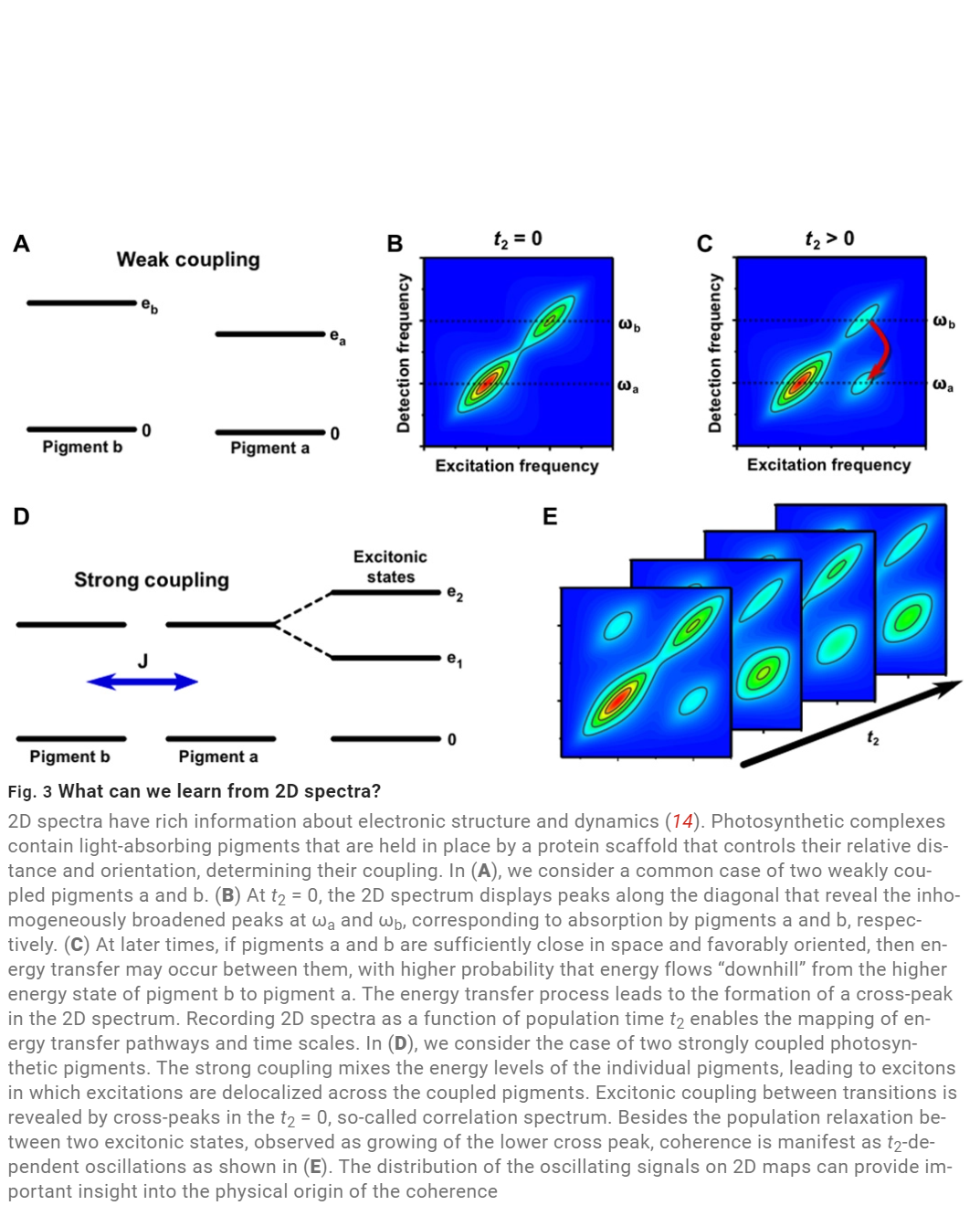
The coherent patterns that are thought to be directly connected to energy transmission are superpositions of several excited states. In a transitory absorption experiment, for example, between the pump and probe pulses, these superpositions, which are nonstationary, evolve. While any pair of system eigenstates, such as excitonic and vibronic, can be superimposed using the right optical pulses, superpositions of excitonic states have been regarded as particularly significant in the context of energy transfer. These have been referred to as electronic or excitonic coherences in the literature. These particular coherences will be referred to as interexciton coherences in this context. They develop as damped oscillations in line with the energy disparities between the system eigenstates involved, just like optical coherences.
The dephasing time of these interexciton coherences depends on a variety of variables, such as the magnitude of the bath interaction, the overlap of the exciton wave functions, and the duration of the involved states. Fast-decaying optical coherence (seen as broad homogenous line forms) also denotes fast interexcitonic coherence decay because the degree of coupling to the bath affects the dephasing of both optical and interexcitonic coherences. The precise link to be made relies on the level of exciton localization and bath dynamics, and is described in more detail below.
What we consider to be a concrete and helpful definition of coherence as applied in ultrafast spectroscopic research is given in the succinct statement above. Keep in mind that these facts hold true for both classical and quantum representations, and it turns out that the correlation between coherence in PPCs and classical oscillators is very accurate (vide infra). Where do we find quantumness in biology, nevertheless, is still an open subject. The world is undoubtedly regulated by the wave characteristics of matter at the scale of atoms. The "genuine" quantum reality is simply a construct generated from the classical biological observables. But given that much of the "strangeness" of quantum mechanics is eliminated in the traditional, macroscopic domain of biological systems, which truly quantum phenomena are still significant there?
