QCD AT HIGH TEMPERATURE
It goes without saying that high temperature QCD behaviour is interesting. It answers the innocent question: What happens if you keep turning the heat up? Additionally, it describes how matter behaved at pivotal moments right after the Big Bang. Additionally, it is a topic that may be explored experimentally via high-energy collisions of heavy nuclei. (See page 20 of PHYSICS TODAY, May.) The Relativistic Heavy Ion Collider at Brookhaven National Laboratory, where experiments are just being started, will be specifically devoted to this form of physics. see the below picture for details.

In order to clear up any misunderstandings, I should clarify that I'm assuming a very low net baryon density (quarks minus antiquarks) when I discuss high-temperature QCD in this post. In contrast, I mean a high net density of quarks at low temperature, which is far higher than the usual density of cold nuclear matter. The phase diagram for hadronic matter is typically assumed to have temperature and net baryon density as its two independent variables.
At very high temperatures, asymptotic freedom suggests that QCD physics becomes more straightforward. If you attempted to construct the high-temperature phase by taking into account the generation and interaction of all the various mesons and baryon resonances that are energetically accessible at high temperature, it would seem absurd. We employ a method that is frequently helpful in theoretical physics in an effort to get around this intimidating jumble. I refer to it as the Jesuit Stratagem since it is based on what I understand to be one of the Order's core beliefs: "It is more wonderful to ask forgiveness than permission." The tactic instructs you to make unambiguous, simplifying assumptions, determine their ramifications, and make sure there are no inconsistencies.
Gluons and free quarks are the starting point for high-temperature QCD. The majority of the energy and pressure in an ideal (noninteracting) gas of quarks, antiquarks, and gluons at high temperature will come from particles with huge kinetic and potential energies. How are these particles affected by interactions? Well, a high momentum transfer interaction is necessary to significantly deflect such a particle. However, asymptotic freedom informs us that such interactions are uncommon since they are controlled by relatively weak coupling. Therefore, interactions do not really render the entire picture inaccurate. A nearly perfect gas of quasiparticles results from treating the hadron jets produced by quarks, antiquarks, or gluons as quasiparticles "dressed" in hadronic clothing. It would appear that ignoring the interactions was a good place to start. The ruse was successful.
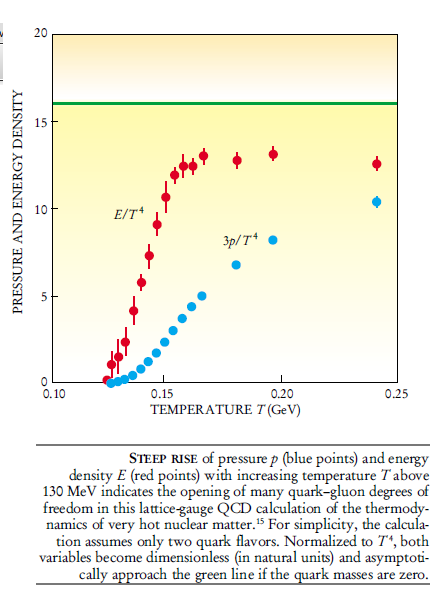
Amazingly, another item that can be determined directly from the equations using sophisticated computers is the thermodynamic behaviour of QCD as a function of temperature. The below demonstrates how the qualitative expectations were amply justified. The only significant representation at "low" temperatures (≂150 MeV or 1.5x1012 K) is the spinless pi mesons:π+,π-,π0 which represent three degrees of freedom. But given that there are three different types of light spin-1/2 quarks, each of which has three colours, we come to expect far more degrees of freedom from a quark-gluon description. Then, instead of the pions' three degrees of freedom, you have 52 if you add eight gluons with two polarisation states, antiquarks, and two spin orientations. As a result, we expect that, at a given temperature, the energy density will greatly increase as you transition from a hadron gas to a quark-gluon plasma. And that is what the below figure's computations demonstrate.
What about actual tests? Unfortunately, we can only reach the quark-gluon plasma by creating tiny, fleeting nuclear fireballs, of which we only observe the remnants. Complex modelling is required for the data interpretation. There are two levels one may aspire to in the search for proof of the quark-gluon plasma. One could expect to find occurrences at the first level that are exceedingly challenging to understand from a hadronic standpoint yet have a straightforward qualitative explanation based on quarks and gluons. The CERN heavy-ion programme has recently recorded several such phenomena. But there is still a second, harder level that will be difficult in the future. One may generate quantitative predictions for the emission of several types of "hard" radiation from a quark-gluon plasma using fundamental parts of QCD theory, similar to those I addressed in connection with jets. Until some of these predictions are verified by experiment, we will not have done justice to the idea of a weakly interacting plasma of quarks and gluons.
