QCD Describing Reality - Quarks & Gluons
The technique that gives each of its Feynman diagrams, which represent potential processes in spacetime, a probability amplitude summarises the physical content of quantum electrodynamics. The interaction vertices of the kind shown at left, which represent a point-charged particle (lepton or quark) radiating a photon, are connected to create the Feynman graphs. A kinematic "propagator" factor for each line and an interaction factor for each vertex are multiplied together to obtain the amplitude. A particle is replaced by its antiparticle when a line's direction is reversed.
The following summarises quantum chromodynamics, but uses a more complex collection of components and variables. The colour charge carried by quarks and antiquarks is one positive (negative) unit. An SU(3) octet of 8 physical gluon types is formed by linear superpositions of the nine different potential gluon colour combinations that are illustrated below.
The existence of vertices describing the direct interactions of colour gluons with one another is a qualitatively novel aspect of QCD. In contrast, photons only couple to electric charge-which they do not themselves carry.

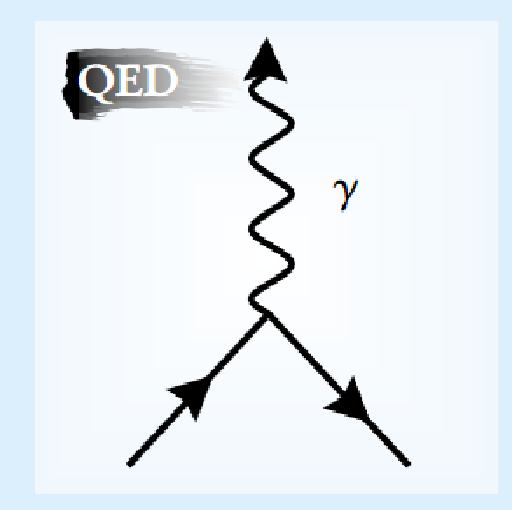
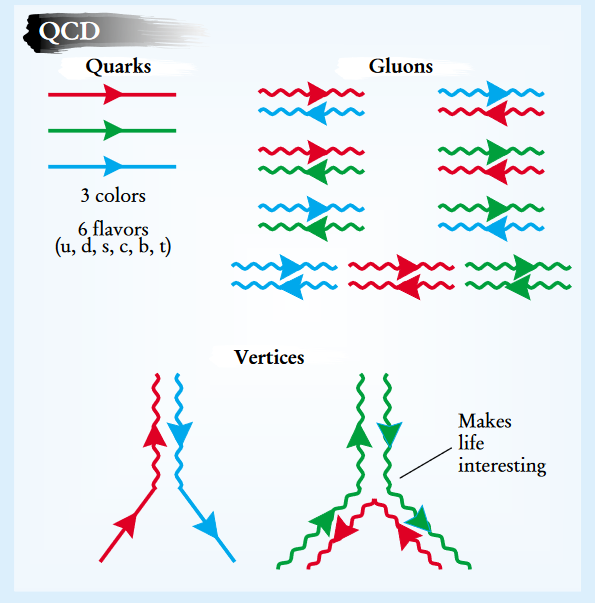
It seems much rather strange at first to propose that the equations in the above picture, or, alternatively, the images in the picture can describe the intensely interacting environment outside of the box. particles. None of the actual particles we've observed none of the particles that do so appear in the box. There have been reports of the box. Specifically, we've never observed particles with a little electric charge, which We still attribute to the quarks, though. Of course, we have never encountered any massless particles like gluons. balancing distant powerful forces. in order for QCD to explain why quarks and gluons exist in the world. Ons are not possible as lone particles. The alleged confinement issue is that.
In addition to confinement, there is another qualitative distinction between the universe of quarks and gluons and the perceived reality. This distinction is equally important but far more difficult to articulate. The phenomenological arguments will not be fully addressed here, but I can present the core of the issue in its final, theoretically sanitised version. The phenomenology suggests that the u and d quarks must have extremely modest masses if QCD is to accurately explain the universe. But if these quarks do really have incredibly small masses, then the QCD equations also contain some other symmetries known as chiral symmetries (after chiros, the Greek word for hand). The right-handed quarks can undergo different transformations thanks to these symmetries, including spinning the left-handed quarks and standard right-handed screws, respectively, to their motion.
However, the strongly interacting particles that have been detected do not exhibit this symmetry; they do not exist in opposite-parity pairs. Therefore, much as rotational symmetry is spontaneously broken in a ferromagnet, the chiral symmetry must be disrupted if QCD is to accurately describe reality.
It is obvious that connecting the stunningly straightforward ideas that underpin QCD to the realm of observed facts is a very difficult task. Three fundamental strategies have been used to overcome this challenge:
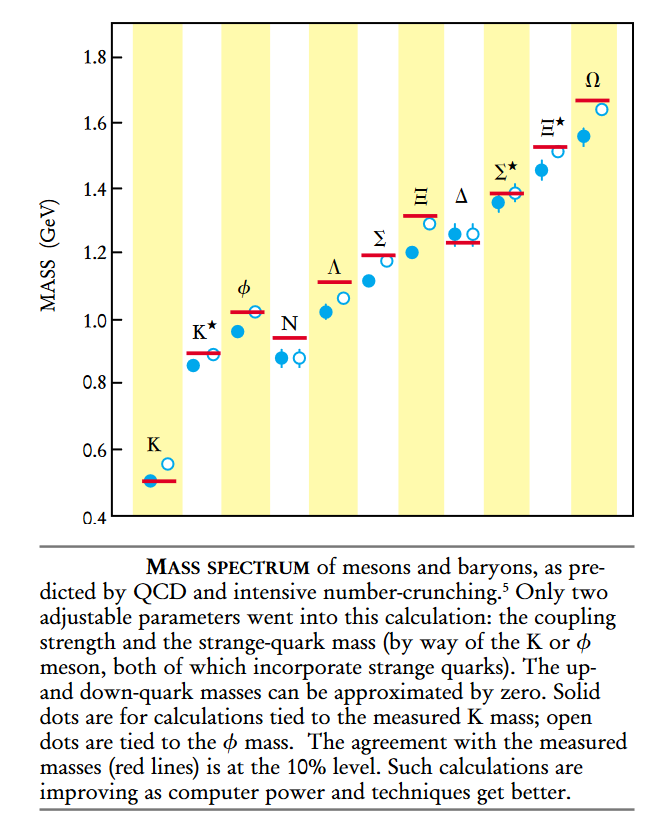
➤ The first strategy is to just solve the equations and grab the bull by the horns. That is difficult. Because the solution must have qualities (such as confinement and chiral-symmetry breaking) that are considerably different from what the equations intuitively seem to suggest and must reflect a rich, complicated phenomenology, it had better not be too simple. Fortunately, some of the most important QCD predictions can now be calculated directly thanks to today's highly advanced computers. The estimated masses 5 of an astounding range of hadrons are contrasted with their observed values in the above picture, which displays benchmark results. The consensus is reassuring.
These computations evince unequivocally that confinement and chiral symmetry breaking are outcomes of resolving the QCD equations. The computations do not reveal any fractionally charged particles, massless gluons, or larger multiplets that would suggest continuous chiral symmetry. There is nothing more or less than the observed particles with the necessary characteristics.
Like electrons, quarks are point particles with a spin of 1/2. However, they contain colour charge rather than electric energy. To be more precise, quarks carry fractional elec- tric charge in addition to their colour charge (+ 2e/3 for the u, c, and t quarks and - e/3 for the d, s, and b quarks).
Even if the results of these and other enormous numerical calculations are amazing and helpful, they do not satisfy every request. The known numerical methodologies become unfeasible for a variety of physically intriguing QCD topics. Additionally, having our computers behave as oracles and provide answers without any justification is not wholly satisfying.
➤ The second strategy is to give up on trying to solve QCD directly and instead concentrate on models that are easier to manage while still having some striking similarities to the actual thing. Theorists have investigated several simplified alternatives, such as models with supersymmetry or different gauge groups that are similar to QCD in less dimensions. In this approach, many enlightening revelations have been attained. Such modelistic discoveries, however, are not by definition adapted to a direct confrontation with physical reality.
➤ The third strategy, which will be the focus of the remaining paragraphs of this essay, is to think about real-world situations where the equations somehow get easier.
