QUANTUM ELECTRODYNAMICS -
FEYNMAN RULES & DIAGRAMS
Introduction
⇒ Feynman Diagrams are pictorial representations of the interactions of subatomic particles
⇒ For example, this shows a Feynman Diagram of beta (β-) decay (nuclear equations):
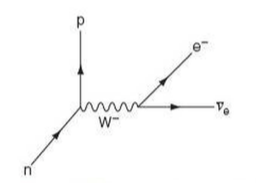
⇒ Usually, Feynman Diagrams are read from left to right
⇒ So, here, we can see a neutron decaying into a proton and a W- exchange particle, which subsequently decays into an electron and an electron anti-neutrino
⇒ Thus, this is showing a weak interacting and can be written as an equation as follows:
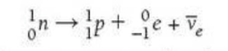
⇒ The big advantage of Feynman Diagrams is that it not only tells you what goes into the interaction and what comes out, but also what goes on during the interaction itself
Rules of Feynman Diagrams
⇒ Particles are represented using straight lines with arrows on them
⇒ Exchange particles are represented using wavy lines
⇒ They usually move from left to right, with the first action happening on the left and the last happening on the right (although this isn't always the case, with some moving vertically instead)
⇒ Particle creation and annihilation occurs where the lines come together
⇒ Exchange particles usually move left to right unless there is an arrow above the wavy line that indicates it is moving in a different direction
Examples of Feynman Diagrams
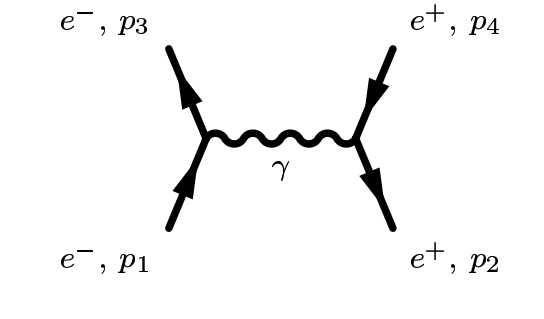
Two Electrons Scattering Off Each Other
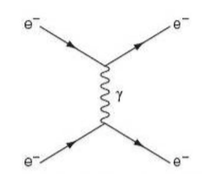
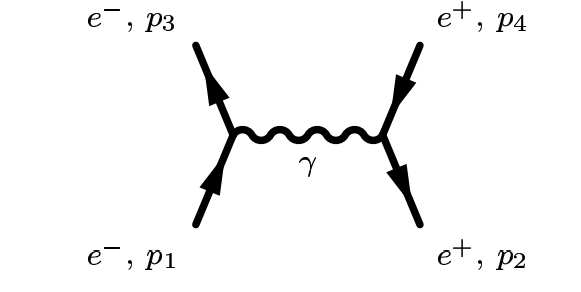
⇒ In this diagram we can see that two electrons meet, exchange photons, and then scatter away from each other
⇒ The photon symbol (γ) shows that this is an example of electromagnetic interaction
β+ (positron) radioactive decay
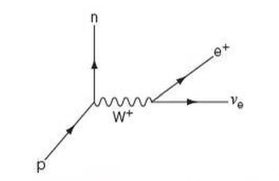
⇒ In this diagram, we can see a proton decays into a neutron and a W+ exchange particle, which subsequently decays into a positron and an electron neutrino
⇒ This is an example of weak interaction (like the β- decay, above)
⇒ The equation for this radioactive decays is as follows:
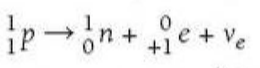
⇒ Note: β- decay is negative so it involves e-, an anti-neutrino and W-, whereas β+ decay is positive so involves e+, a neutrino and W+
Electron Capture
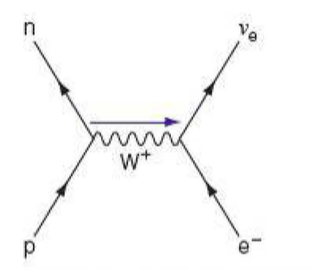
⇒ This is also an example of weak interaction
⇒ Through electron capture, an electron is absorbed by a proton within a nucleus
⇒ The proton decays into a neutron and a W+ exchange particle. The W+ exchange particle interacts with the electron forming an electron neutrino
- As the proton acts on the electron, the exchange particle moves from left to right
⇒ The equation for this is as follows:
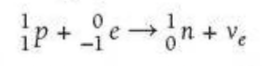
Electron-proton collision
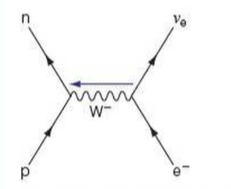
⇒ When a proton and an electron collide at very high-speeds they will transfer a W- particle, again indicating a weak interaction
⇒ The proton decays into a neutron and the electron decays into an electron neutrino
- This time, as it is the electron that is colliding with the proton, the exchange particle moves from right to left
⇒ The equation for this is as follows:

Proton-Neutron bound by a gluon
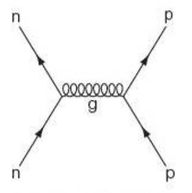
⇒ As a gluon exchanges between protons and neutrons continuously, it binds them together
⇒ This symbol for this exchange particle (i.e. the gluon) is different than that used for other exchange particles
⇒ This is an example of strong interaction

The formula for creating an amplitude Μ from a Feynman diagram can be found in the Feynman rules.
- Step 1: create a Feynman diagram with the fewest number of vertices possible for the particular process of interest. There could be several.
- Step 2: label the four-momentum of each line in each Feynman diagram, being sure to enforce four-momentum conservation at each vertices. Keep in mind that arrows are only visible on fermion lines and that they indicate particle flow rather than momentum.
-
The amplitude depends on
1. Vertex factors
2. Propagators for internal lines
3. Wavefunctions for external line
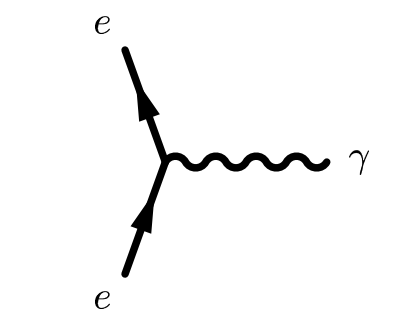
Vertex Factors
- Every QED vertex contributes a factor of igeγμ
- ge is a dimensionless coupling constant and is related to the fine-structure constant
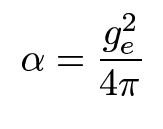
Propagators
- Every QED vertex contributes a factor of igeγμ
- Each internal photon connects two vertices of the form igeγμ and , so we should expect the photon propagator to contract the indices μ and ν
- Internal fermions have a more complicated propagator:


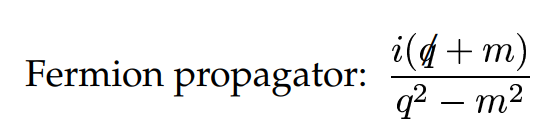
The sign of q matters here - we take it to be in the same direction as the fermion arrow.
External Lines
- Since both the vertex factor and the fermion propagators involve 4X4 matrices, but the amplitude must be a scalar, the external line factors must sit on the outside
- Work backwards along every fermion line usin
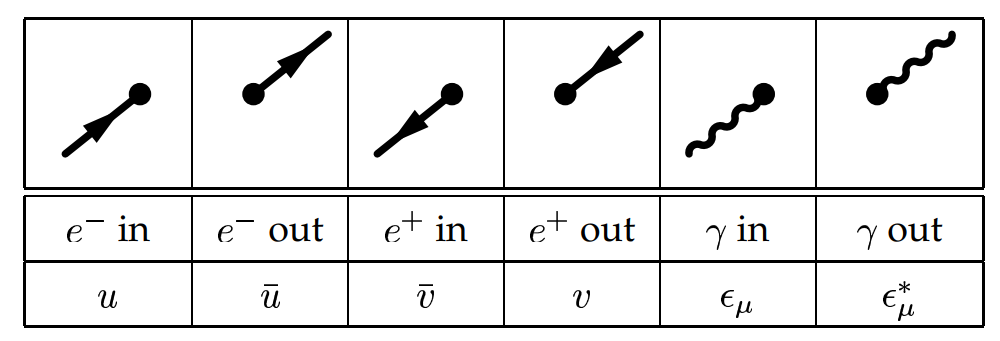
Matrix Elements


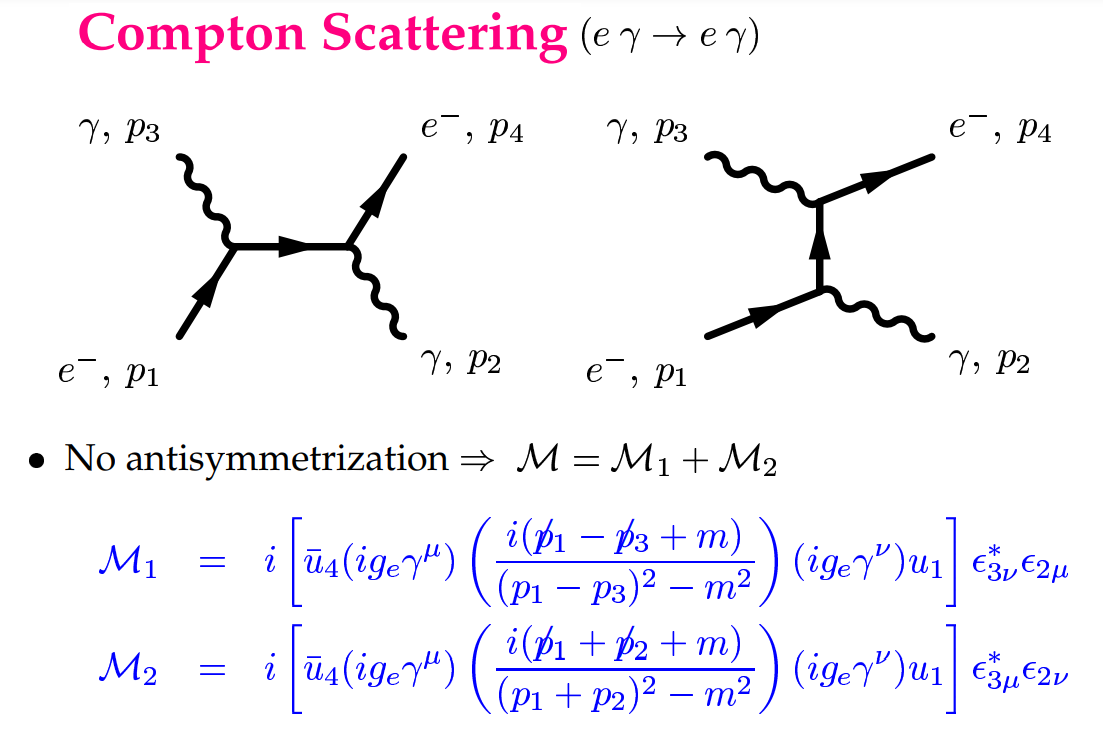
- Step 4: The total amplitude is the coherent sum of each diagram's component amplitudes.
- Step 4a: Antisymmetrization. Between diagrams that only differ in the swap of two identical fermions, use a minus sign.