QUANTUM ELECTRODYNAMICS - THE ELECTROMAGNETIC VERTEX
All particle reactions in electrodynamics are brought about by the fundamental weak, electromagnetic, and strong forces between the elementary particles involved. A convenient way of illustrating this is to use Feynman diagrams. There are mathematical techniques associated with these, which enable them to be used to calculate the quantum mechanical probabilities for given reactions to occur, but in this article we will simply use them as a convenient pictorial description of reaction mechanisms. We first illustrate them for the case of electromagnetic reactions, which arise from the emission and/or absorption of photons.
For example, the dominant interaction between two electrons is due to the exchange of a single photon, which is emitted by one electron and absorbed by the other. This mechanism, which gives rise to the familiar Coulomb interaction at large distances, is illustrated in the Feynman diagram (Fig. 1a). In such diagrams, by convention, the initial particles are shown on the left and the final particles to the right. Spin-1/2 fermions (such as the electron) are drawn as solid lines and photons are drawn as wiggly lines. The arrow heads pointing to the right indicate that the solid lines represent electrons. In the case of photon exchange between two positrons, which is shown in Fig. 1b, the arrow heads on the antiparticle (positron) lines are conventionally shown as pointing to the left.
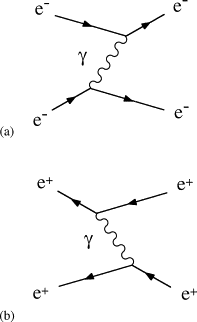
FIGURE 1. Feynman diagrams for (a) electron–electron elastic scattering and (b) positron–positron elastic scattering, via the exchange of a single photon.
The dominant contributions to the annihilation reaction e+ e− → γγ are shown in Fig. 2. In the first diagram, the positron emits a photon and then annihilates with an electron to produce the second photon; in the second the electron emits the photon before annihilating with the positron to produce the second photon. (In practice, it is usual to draw just one of these diagrams, leaving the other implied.) In interpreting these diagrams, it is important to remember that the direction of the arrows on fermion lines do not indicate their direction of motion, but merely whether the fermions are particles or antiparticles; and that the initial particles are always to the left and the final particles to the right.
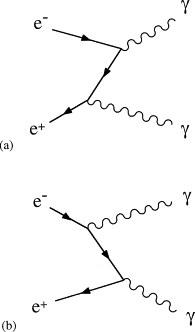
FIGURE 2. The dominant Feynman diagrams for electron–positron annihilation to give two photons in the final state.
A feature of these diagrams is that they are constructed from a single fundamental three-line vertex. This is characteristic of electromagnetic processes. Each vertex has a line corresponding to a single photon being emitted or absorbed; while one fermion line has the arrow pointing toward the vertex and the other away, guaranteeing charge conservation at the vertex. For example, a forbidden vertex like Fig. 3 would correspond to a process in which an electron emitted a photon and turned into a positron, violating charge conservation. Associated with each vertex of a Feynman diagram is a dimensionless parameter, the so-called coupling constant, which represents the basic strength of the interaction. For electromagnetic interactions like Figs. 1 and 2, this is the fine structure constant α, defined by
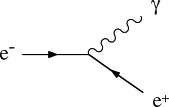
FIGURE 3. A forbidden electromagnetic vertex in which both arrows point into the vertex. Such a vertex would violate electric charge conservation.
where e is the charge on the proton, c is the speed of light, ε0 is the permittivity of free space, and .
The number of vertices in any diagram is called the order n, and when the probability associated with any given Feynman diagram is calculated, it always contains a factor of αn. The single-photon exchange diagrams of Fig. 1 thus contain a factor of α2. In addition, one can easily draw diagrams corresponding to two-photon exchange contributions to the same processes, which contain four vertices, as illustrated in Fig. 4. The contribution from two-photon exchange is therefore of order α4 and is very small compared to the contribution from single-photon exchange. This is again a general feature of electromagnetic interactions. Because the fine structure constant is very small, only the lowest-order diagrams which contribute to a given process need be taken into account, and more complicated higher-order diagrams with more vertices can to a good approximation be ignored.
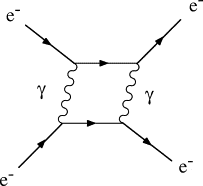
FIGURE 4. A two-photon exchange contribution to electron–electron scattering. Because the fine structure constant α is so small, this makes a very small contribution compared to one-photon exchange, and can usually be ignored.
Finishing Touch:
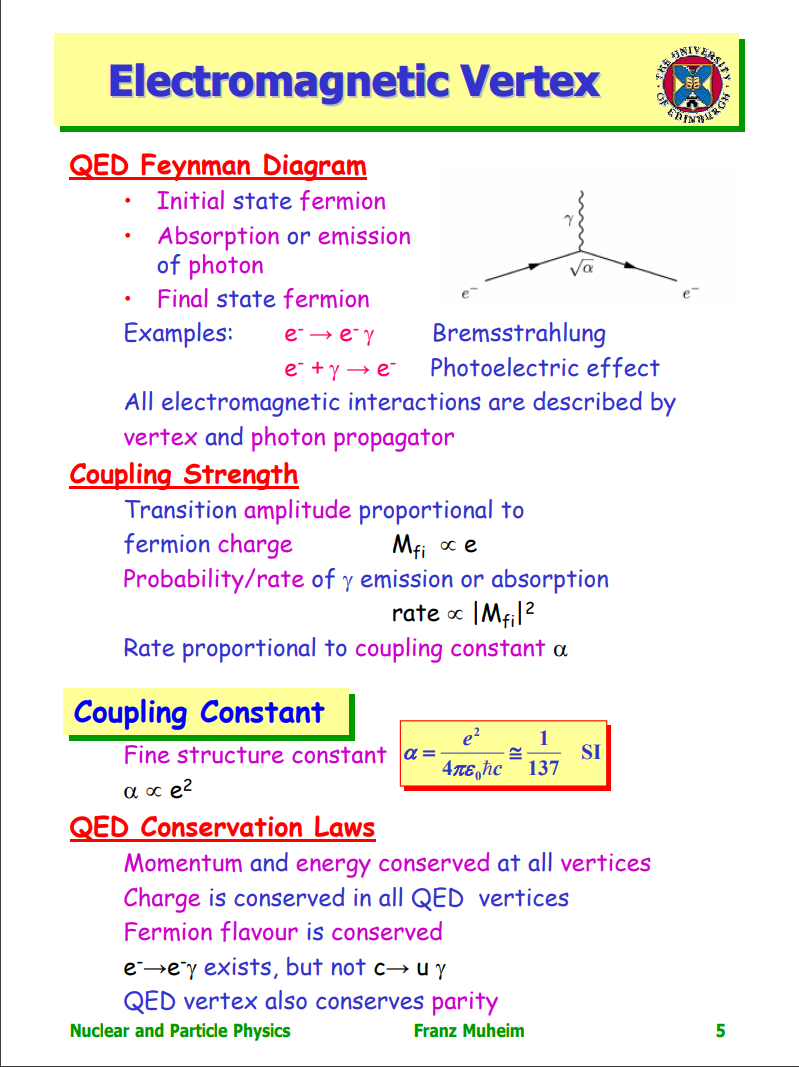
➤ The electromagnetic interaction is described by the photon propagator and the vertex:
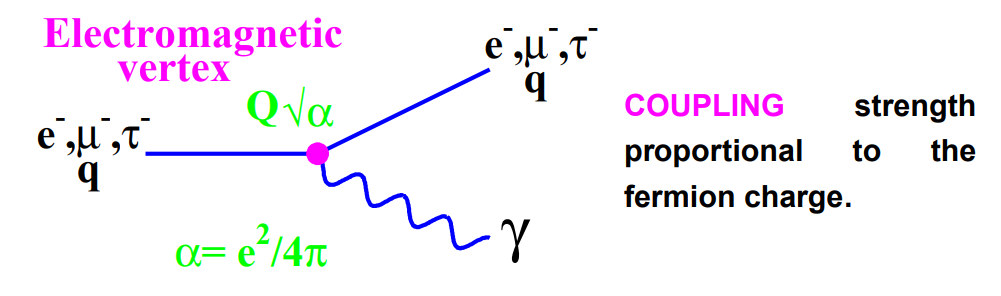
➤ All electromagnetic interactions can be described in terms of the above diagram
➤ Always conserve energy and momentum + (angular momentum, charge)
➤ QED Vertex NEVER changes flavour i.e.

➤ QED Vertex also conserves PARITY

➤ The coupling constant is proportional to the fermion charge.
➤ Energy, momentum, angular momentum, parity and charge always conserved
➤ QED vertex never changes particle type or flavour
