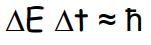QUANTUM ELECTRODYNAMICS - VIRTUAL PARTICLES
In QED (Quantum ElectroDynamics) during the exchange of four-momentum between the two particles, The velocity of the intermediary particle exceeds the speed of light. (Four-momentum means that in special relativity, four-momentum (also called momentum–energy or momenergy) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime.)
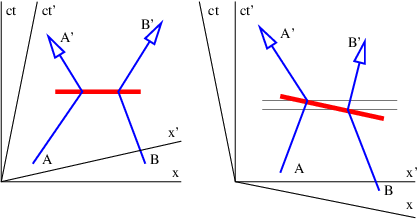
This is reflected in the fact that different reference frames yield contradictory results as to whether the intermediary particle moves from A to B or B to A. These difficulties turn out to be much less severe than those arising from non-locality. Let us address them in sequence.
For sake of definiteness, let us view the emission of particle C by particle A in a reference frame in which the velocity of particle A is just reversed in the emission process. In this case the four-momentum before the emission is \(\mathrm{p}_{\mathrm{A}}=(\mathrm{p}, \mathrm{E} / \mathrm{c}), \text { where } \mathrm{E}=\left(\mathrm{p}^{2} \mathrm{c}^{2}+\mathrm{m}^{2} \mathrm{c}^{4}\right)^{1 / 2}\). After the emission we have \(\mathrm{p}_{\mathrm{A}}^{\prime}=(-\mathrm{p}, \mathrm{E} / \mathrm{c})\). Conservation of four-momentum in the emission process requires that
\[\underline{p}_{A}=\underline{p}_{A}^{\prime}+\underline{q}\label{14.20}\]
where q is the four-momentum of particle C. From the above assumptions it is clear that
\[\underline{q}=\underline{p}_{A}-\underline{p}_{A}^{\prime}=(p+p, E / c-E / c)=(2 p, 0) .\label{14.21}\]
Suppose that the real, measured mass of particle C is \(\mathrm{m}_{\mathrm{C}}\). This conflicts with the apparent or virtual mass of this particle in its flight from A to B, which is
\[m^{\prime}=(-\underline{q} \cdot \underline{q})^{1 / 2} / c \equiv i q / c\label{14.22}\]
where q ≡|q| is the momentum transfer. Note that the apparent mass is imaginary because the four-momentum is spacelike.
Classically, this discrepancy in the apparent and actual masses of the particle C would simply indicate that the process wasn’t possible. However, recall that the uncertainty principle allows there to be an uncertainty in the mass if it doesn’t persist for too long in terms of the proper time interval along the particle’s world line. The statement of this law is \(\Delta \mu \Delta \mathrm{T} \approx 1\). Expressed in terms of mass, this becomes
\[\Delta m \Delta \tau \approx \hbar / c^{2}\label{14.23}\]
Let us convert the proper time to an interval since the world line of particle C is horizontal in the reference frame in which we are viewing it. Ignoring the factor of i, \(\Delta \mathrm{T}=\Delta \mathrm{I} / \mathrm{C}\). We finally compute the absolute value of the mass discrepancy as follows: \(\left|m_{C}-i q / c\right|=\left[\left(m_{C}-i q / c\right)\left(m_{C}+i q / c\right)\right]^{1 / 2}=\left(m c^{2}+q^{2} / c^{2}\right)^{1 / 2}\). Solving for I yields the approximate maximum invariant interval that particle C can move from its source point while keeping its erroneous mass hidden by the uncertainty principle:
\[\Delta I \approx \frac{\hbar}{\left(m_{C}^{2} c^{2}+q^{2}\right)^{1 / 2}}\label{14.24}\]
A particle forced into having an apparent mass different from its actual mass is called a virtual particle. The interaction shown in figure 14.5 can only take place if particles A and B come closer to each other than the distance ΔI. This argument thus produces an estimate for the “range” of an interaction with momentum transfer 2p and intermediary particle mass mC.
Two distinct possibilities exist. If the intermediary particle is massless (a photon, for instance), then the range of the interaction is inversely related to the momentum transfer: \(\Delta \mathrm{I} \approx \hbar / \mathrm{q} .\). Thus, small momentum transfers can occur at large distances. An interaction of this type is called “long range”. On the other hand, if the intermediary particle has mass, the range is simply \(\Delta \mathrm{I} \approx \hbar / \mathrm{m}_{\mathrm{C}} \mathrm{c} \text { when } \mathrm{q} \ll \mathrm{m}_{\mathrm{C}} \mathrm{C}\). The range is thus constant and inversely proportional to the mass of the intermediary particle for low momentum transfers. For large momentum transfer, i. e., when \(\mathrm{q} \gg \mathrm{m}_{\mathrm{C}} \mathrm{C}\), the range decreases from this value with increasing momentum transfer, as in the case of a massless intermediary particle.
Virtual Particles and Gauge Theory
According to quantum mechanics, particles are represented by waves. The absolute square of the wave amplitude represents the probability of finding the particle. In gauge theory the potential four-momentum performs this role for the virtual particles intermediary interactions. Thus a larger potential four-momentum at some point means a higher probability of finding the related virtual particles at that point.
The theory of potential momentum is only one of three ways in which the idea of potential energy can be extended to the relativistic case. This theory is called gauge theory for obscure historical reasons. Gauge theory is important because electromagnetism as well as the theories of weak and strong sub-nuclear interactions are all of this type.
Gravity is the only fundamental force that does not take the form of a gauge theory. Instead, gravity takes the form of one of two other possible relativistic extensions of potential energy. This theory is called general relativity. The gravitational force in general relativity can be interpreted geometrically as a consequence of the curvature of spacetime. Mathematically, it is far too difficult to pursue here.
The third relativistic extension of potential energy considers potential energy to be a field which alters the rest energy of particles. High energy physicists believe that the elementary particles gain their mass by this mechanism. The field is called the Higgs field after the English physicist who first proposed this theory, Peter Higgs. The recent discovery of the Higgs boson at CERN’s Large Hadron Collider in Geneva, Switzerland supports this idea.
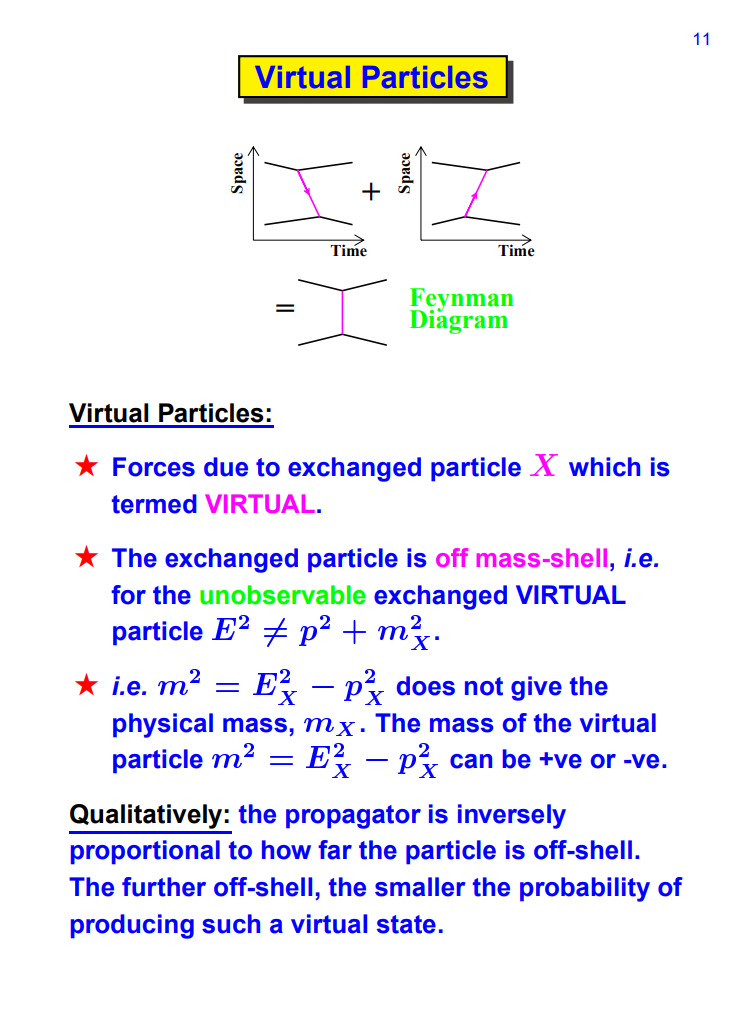
A quantum field theory of the electromagnetic force is known as quantum electrodynamics (or QED). The classical theory of electromagnetism would explain the force between two electrons, for instance, as originating from the electric field each electron produced at the site of the other. The Coulomb's law can be used to compute the force. The force between the electrons is represented by the quantum field theory method as an exchange force resulting from the interchange of virtual photons. Feynman diagrams are used to illustrate it.
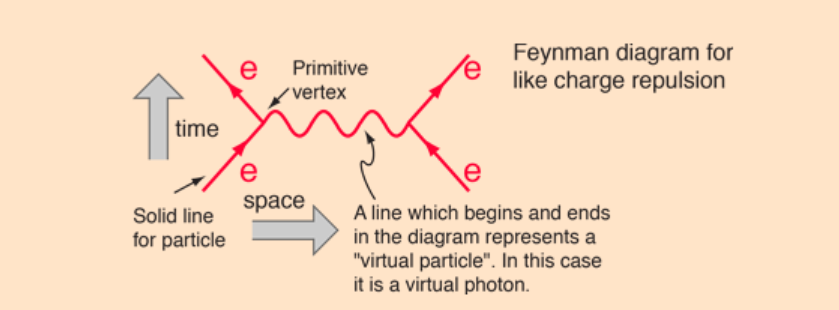
This picture depicts the electron interaction in which two electrons enter, exchange a photon, and then emerge, with time moving upward. The strength of the force can be computed in a series of stages that allocate contributions to each of the many kinds of Feynman diagrams connected to the force using a mathematical technique called the Feynman calculus.
All electromagnetic events involving charged fundamental particles like electrons and positrons, as well as related phenomena like pair creation, electron-positron annihilation, Compton scattering, etc., are covered by QED. It was used to precisely simulate several quantum events, like the Lamb shift and the electron's anomalous magnetic moment, for which there were no classical counterparts. The first effective quantum field theory was QED, which integrated concepts like particle creation and annihilation into a self-consistent framework. The creation of the theory served as the foundation for Richard Feynman, Julian Schwinger, and Sin-itero Tomonaga's 1965 Nobel Prize in Physics.
Quantum electrodynamics is the branch of physics that explains how charged particles interact with light. The application of quantum theory to fields of force, starting with electromagnetic fields, is known as quantum electrodynamics (QED).
A quantum theory of the interactions between charged particles and the electromagnetic field is known as quantum electrodynamics, or QED. It provides a mathematical description of all interactions between charged particles as well as between light and matter. In that each of QED's equations incorporates Albert Einstein's theory of special relativity, it is a relativistic theory. Since atoms and molecules behave predominantly in electromagnetic ways, all of atomic physics can be thought of as a test lab for the hypothesis.
With the discovery of an equation describing the motion and spin of electrons in 1926 that combined the concepts of the quantum theory and the theory of special relativity, British scientist P.A.M. Dirac set the groundwork for quantum electrodynamics (QED). Independently of one another, Richard P. Feynman, Julian S. Schwinger, and Shin'ichiro Tomonaga refined and fully developed the QED theory in the late 1940s. The foundation of QED is the hypothesis that charged particles, such as electrons and positrons, interact through the emission and absorption of photons, the light particles that carry electromagnetic forces. Since their existence goes against the conservation of energy and momentum, these photons are virtual, which means that there is no way to observe or detect them.
According to QED, charged particles interact through the exchange of virtual photons, which act exclusively as momentum and force carriers and do not exist outside of the interaction.
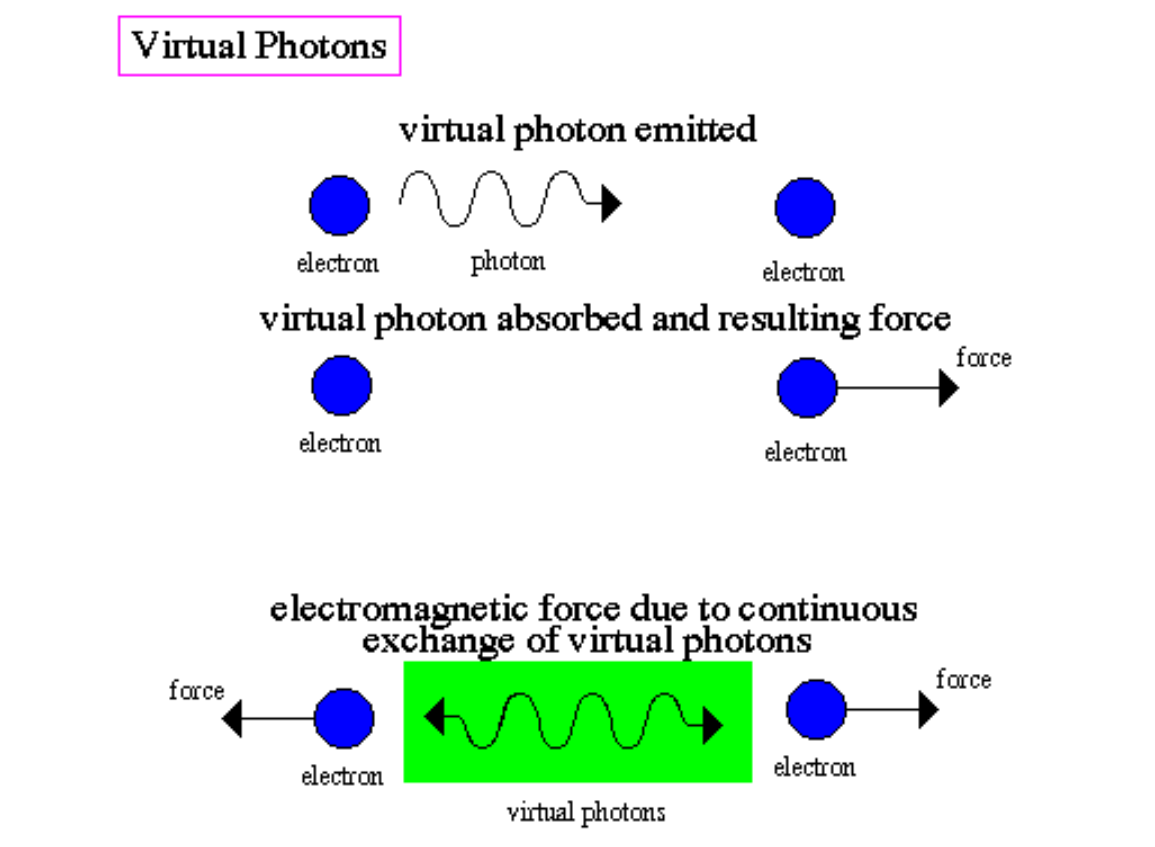
Observe how the interaction is caused by the photons coming into touch directly, eliminating action at a distance. The theories of weak and electromagnetic interactions were unified in the 1960s as a result of a formulation of QED. At extraordinarily high temperatures, such those observed in the early Universe and simulated in particle accelerators, the new force known as electroweak emerges. The electromagnetic and weak forces become symmetric at this point, acting as though they are one force. This is known as unification. The idea that the weak, electromagnetic, and strong forces can be unified into what is known as the Standard Model of matter was first proposed by electroweak unification.
Due to QED, the electromagnetic and weak forces were combined, suggesting that under extremely high temperatures and energies, all forces constitute one force (like with the Universe formed)
- the quantum electrodynamics-understood through the combination of light and charged particles
- The assumption that virtual photons transmit electromagnetic force is fundamental to QED.
- However, because their existence violates conservation laws, virtual means they cannot be seen or detected.
Electromagnetic Interaction
- Virtual photon exchange is what causes the forces between two charged particles.
- The electromagnetic interaction is mediated by photons.
- No distant action is necessary!
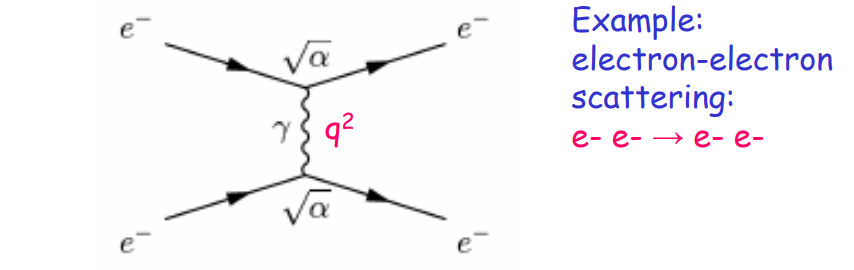
Finishing Touch - Virtual Particles
-
Do not have mass unlike a physical particle.
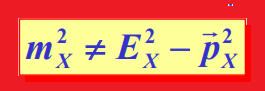
- "Off mass-shell" refers to these virtual particles such as non-zero photons.
-
A virtual particle's 4-momentum is the result of momentum and energy transfers between scattered particles.

-
Virtual mass-squared
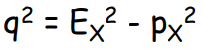
q2 > 0 and q2 < 0 possible. - Propagator: How distant is the particle from the mass-shell
-
Internal lines that are not visible must observe: