Blackbody Radiation :
Light Manifesting As Both Waves And Particles

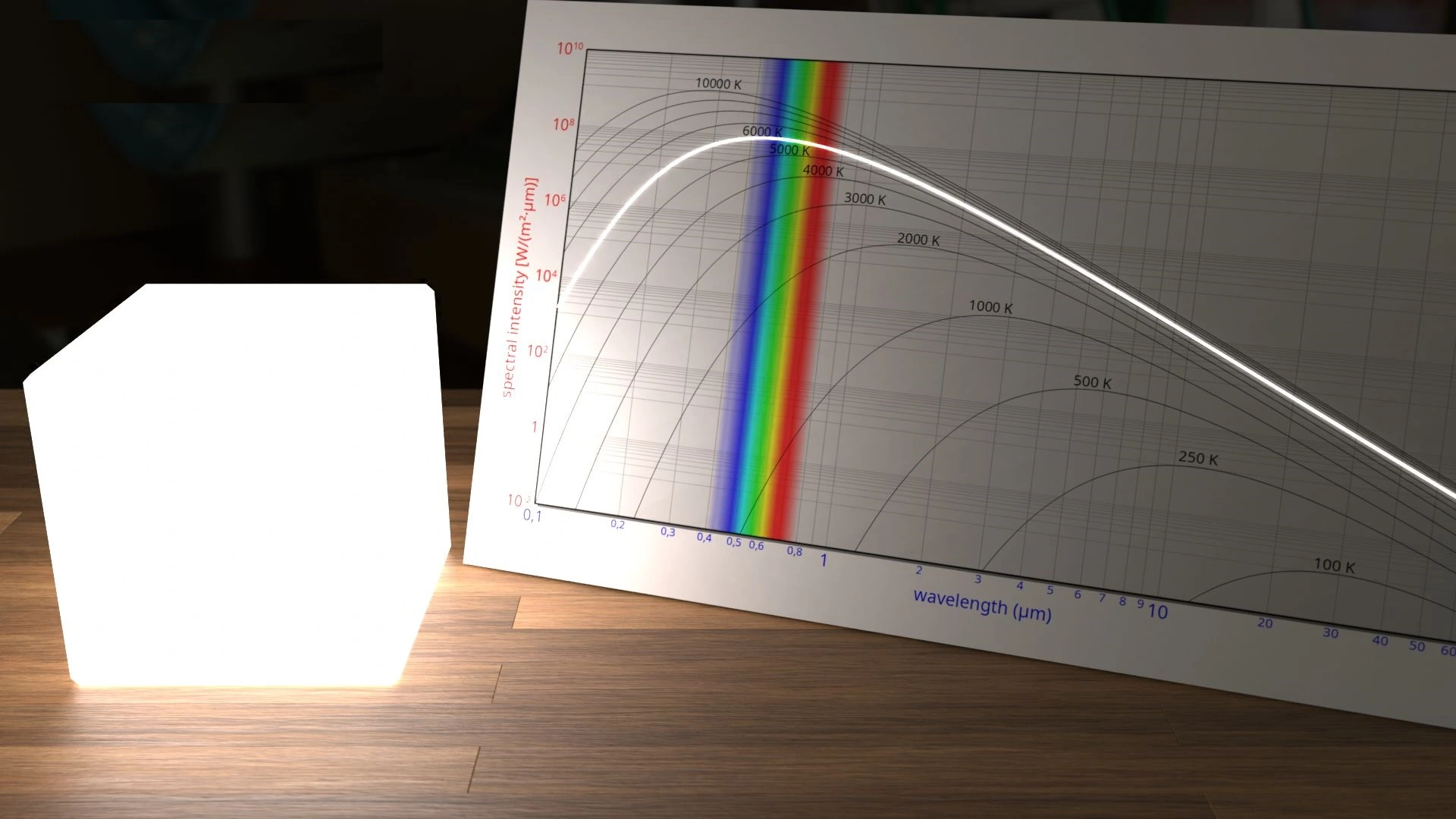
Blackbody radiation is nothing but the phenomena where the surface absorbs all the electromagnetic radiation (all the light) falling upon it. The fact that light can behave like particles is proved experimentally by examining the radiation spectrum of light emitted by every object. In addition to proving the particle nature of light, the investigation on the blackbody radiation gave rise to the field of Quantum Physics.

The Problem Of Blackbody Radiation

Every object above the absolute temperature of zero (0°K) emits radiation in the infrared range. The spectrum of that radiated light was studied by Physicists and they found it to be varying based on the temperature of the object. A perfect blackbody is any object that emits all the light that is incident on it from the environment around it.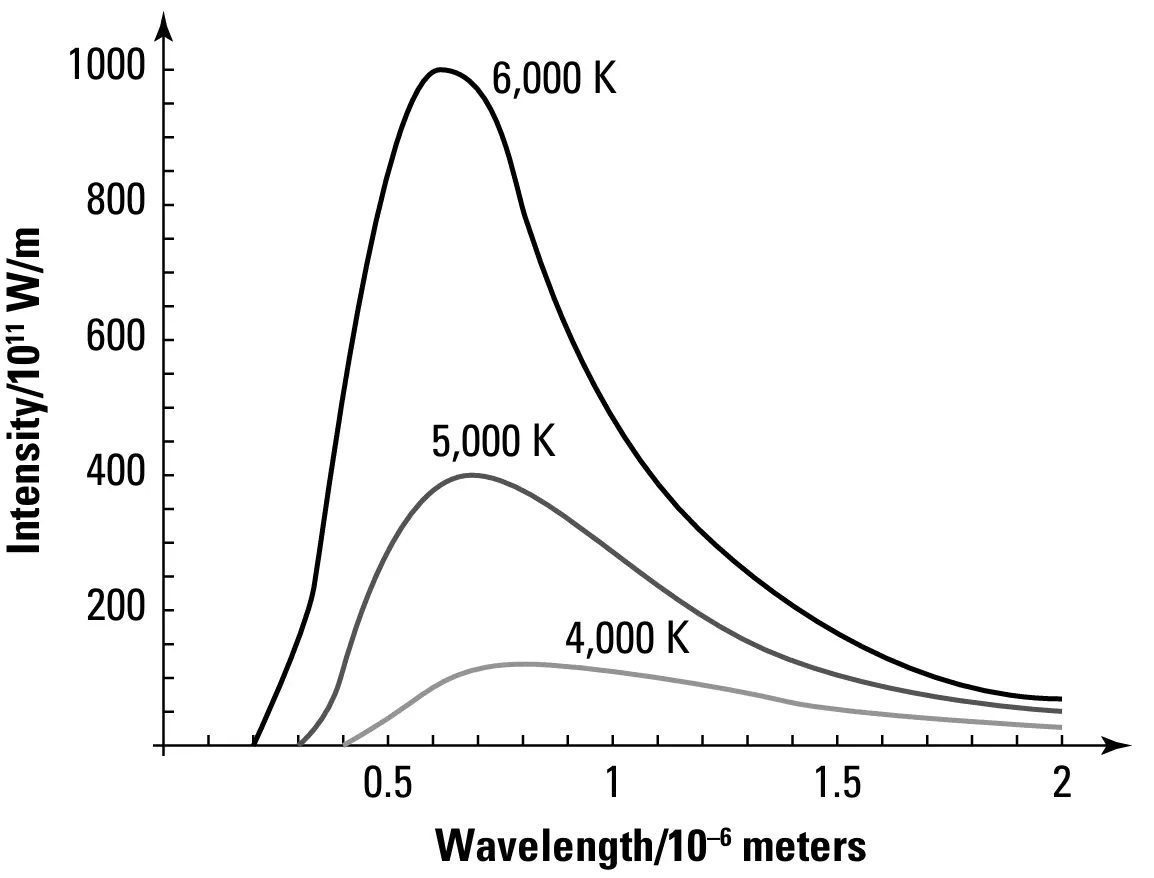

FIGURE-1: The radiation spectrum of a blackbody

The figure-1 shows the spectrum of the emitted light - intensity vs wavelength - from a perfect blackbody (Intensity is the amount of energy radiated per unit area per a second) . If you look at the above figure, you can see that the wavelength decreased with the temperature increasing. Physists tried to explain the spectrum applying the wave nature of light. But all these attempts failed in predicting the spectrum that can match the one actually emitted by the objects.

Max Planck took up this task of how blackbody radiation works. He thought up a radical idea different from the conventional view at that time. His idea was that light can be emitted as a stream of particles in stead of traveling like a wave. His theory considered the object emitting the radiation as a collection of small atomic-sized oscillators and these oscillators can emit radiation of a particular energy which is defined as below:

E=nhν
where n is any positive integer 1,2,3...
ν is the frequency of the oscillator ,
h is a constant that Planck himself invented which is called Planck's constant.
the value of h = 6.626 x 10^-34 J.s

So the energy emitted by any atomic oscillator can only be discrete and is an integer multiple of hν. Other values of energy are not allowed to be emitted. So this discreteness of the system makes it quantized. That was the birth of the Quantum Physics. So for this reason, Max Planck has been renowned as the father of the Quantum Mechanics.

The fact that the atomic-sized oscillators are quantized makes the light emitted quantized also. That means light exists in discrete quantities of energy. As energy is related to wavelength, only specific wavelengths can exist of the light. This was in cotradiction to the then conventional view of light having a continuous spectrum of wavelengths.

So Planck discovered the particle-like nature of light where in each particle of light called "photon" is having its own allowed frequency , wavelength and its own "allowed energy".

Discrete Packets Of Light Energy And The Photoelectric Effect

From Max Planck's discovery of particle-nature of light, It meant that light consists of discrete packets of energy. Using this concept of quantized packets of light energy, Einstein tried to explain the photoelectric effect which is the phenomena in which the electrons are knocked off from the atoms of a metallic plate by photons (which are nothing but the particles of light) hitting that metal plate.

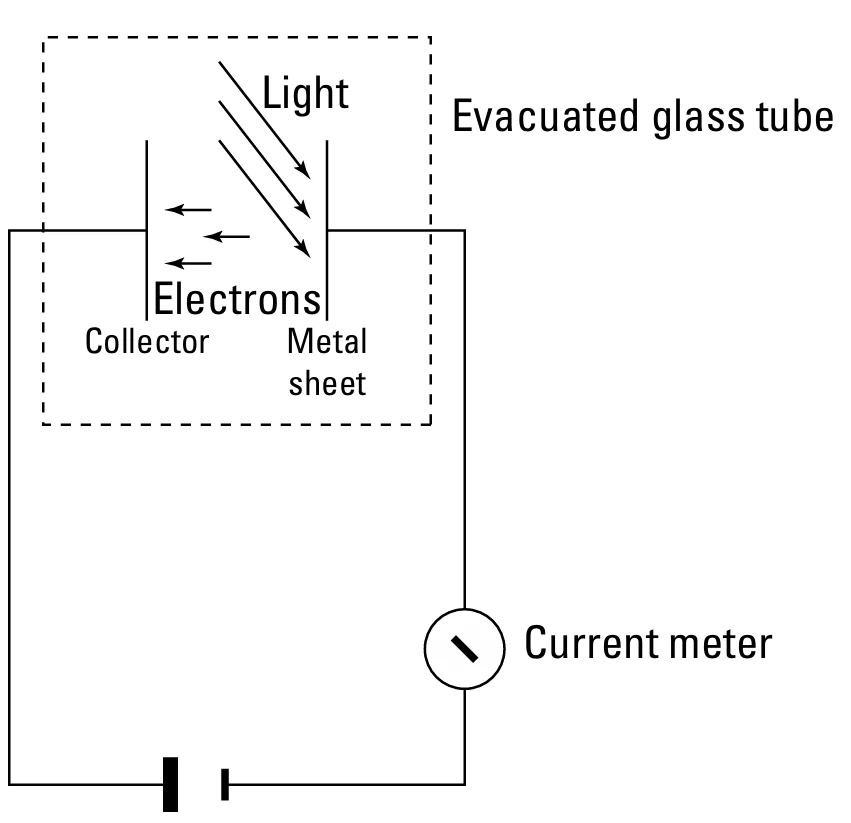
FIGURE-2: Experimental setup for the photoelectric effect

The above image shows the experimental setup for measuring the photoelectric effect. Usually, the electrons are confined to the atoms of the metal plate. Even when a voltage is applied across the collector and the metal plate, they dont leave the metal plate.

But sometimes when a beam of light is flashed upon the metal plate, the photons of the light beam interact with the electrons and give them a little more energy. If the energy given by the photons is much enough, then electrons will gain momentum and break free from the atoms. And these electrons will travel to the other side where the collector which is a positive plate is installed. When the electrons pass from one side to the other side through the vacuum, there is a current flow between the plates and this current can be measured with the meter attached to the plates. So overall, the thing is that when a flash of light is shown on the metal plate, current flows from one plate to the other. It is just that.

You can experiment with this setup with different frequencies of light as well as different intensities. When a high intensity light is flashed on the metal plate, It is expected that electrons will gather energy in some time and leave the atoms. But that is not what has happened in the experiment.

Here are the findings from the experiment:

1. Even if you double the intensity of the light (that means more number of photons emitted per a second), the energy gained by electrons is not more than (in other words, same as) the energy gained when the intensity of the light is low.
2. Even when a low-intensity light is shown upon the metal plate sometimes, electrons will gain enough energy and leave from the atoms of the metal plate instantly. There is no delay in gaining the energy and momentum.

Einstein explained the above scenario by building upon the work of Max Planck and put forth an argument that light does actually consist of discrete packets of energy called "photons".

He proposed that the energy of each photon is equal to : E=hν
where h is Planck' constant (6.626 x 10^-34 Jouls-seconds) and ν is the frequency of the photon.

So this equation tells that the photon's energy is dependent only upon its frequency. When light is flashed upon the metal plate, each electron inside the atoms absorbs one photon. So the energy of the freed-up electron is dependent only on the frequency of the photon. Even if you show light of a high enough frequency at low intensity, electrons will still gain enough energy required to break them free from the atoms. So with high intensity, there will be more electrons released and there will more current.

The energy needed to pull an electron out of the atom is called the "work function" (WF). Part of the photon's energy goes into the work function WF and the remaining part of the eneergy goes into the kinetic energy (KE) of the electron.

Photon's energy E = hν = WF+KE

This equation for the kinetic energy of the electron says that the KE of the electron is dependent only on the frequency of the incident photon - not on the number of photons- and also on the work function of the metal (work function is expressed generally in electron volts (EV) which is the work need to do to move an electron towards the negative plate in a parallel plate capacitor across 1 volt).

Suppose , let us say that you shine your flashlight upon the silver metal. Can it remove the electrons from the atoms of the silver ?

Let us see - the work function (WF) of the silver metal is 4.72 eV. It means that you need that much of energy to remove electrons from the silver metal. So let us calculate the frequency of the light (photons) that can generate the required 4.72 eV energy.

Let us convert the 4.72 eV into joules which is the energy needed. ( 1 eV = 1.60 x 10^-19 Joules)

Work Function (WF) = (4.72) x (1.60 x 10^-19) ≈ 7.55 x 10^-19 J

So it means that the photons that our flashlight gives off should have an energy of 7.55 x 10^-19 Joules.

So let us calculate what is the frequency of the photons to have this much of energy

Energy of photon (E) = hf where h is Planck' constant and f is the frequency.

So f = \(E \over h \)

f = \( {7.55 \times 10^{-19}} \over { 6.626 \times 10^{-34} }\) ≈ 1.14 x 10¹⁵ Hz

So this is the needed frequency of the photons. Let us calculate the wavelength of the photons

c=λf ,

so rewriting it for wavelength λ = \( c \over f \) = \( {3.00 \times 10^8} \over {1.14 \times 10^{15}} \) = 263 nm (nanometers)

So the light that the flashlight gives off should have a wavelength equal to or shorter than 263 nanometers which is in the ultra-violet range. But the flashlight we are using emits light in the visible range. So it is not going to remove the electrons from the silver metal.

Einstein proposed the particle nature of light just theoretically. However it was proved literally with Compton Scattering experiment. Compton did an experiment in which photons collided with electrons and both scattered off.

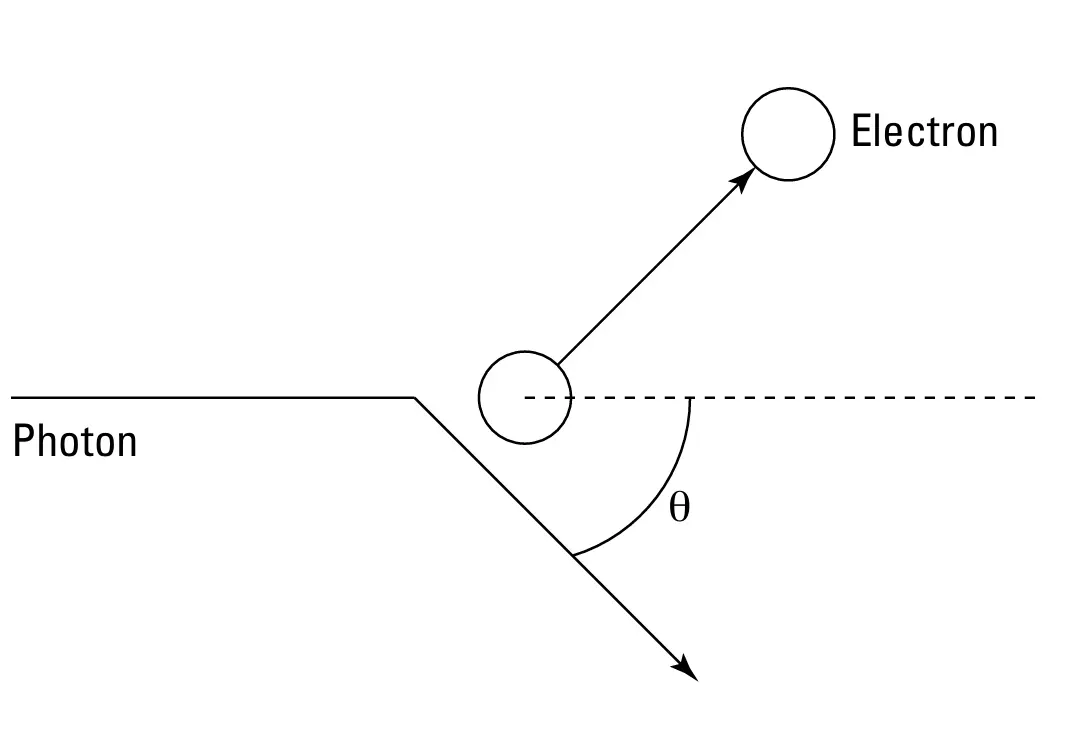
Compton projected beams of X-rays (which are high-energy photons) onto a graphite film. Photons collided with electrons and were scattered off. The frequency of the scattered photons was less than the frequeny of the incident photons. It indicates that the photon transmitted some of its energy to the electron. This collision between the photon and the electron is elastic which means that both the momentum and the energy of the photon and the electron was conserved before and after the collision. You can see the collision between the photon and the electron in the below figure

FIGURE-3: The Compton Scattering

Energy conservation → E_{incident photon} = E_{scattered photon} + KE_{scattered electron}

Similarly,

Momentum conservation → P_{incident photon} = P_{scattered photon} + P_{scattered electron}

The momentum of the electron is mv or in the relativistic form:

\( p = { mv \over { \sqrt{ 1 - {\cfrac{v^2}{c^2} } } } } \)

The above equation is applicable to the electron which has mass, what is the momentum of a photon which does not have any mass?
Let us try to calculate the momentum of the photon. The relativistic energy of the photon:

\( E = { mc^2 \over { \sqrt{ 1 - {\cfrac{v^2}{c^2} } } } } \)

The equation also contains the mass m in it. So to drop out the mass from the equation, we can divide the momentum by the energy which gives the following

\( {\cfrac{P}{E}} = { \cfrac{v}{c^2} } \)

for the photon, v=c , so

\( {\cfrac{P}{E}} = { \cfrac{1}{c} } \)

\( {P} = { \cfrac{E}{c} } \)

and for the photons, E=hf, so

\( {\cfrac{P}{E}} = { \cfrac{1}{c} } \)

\( {P} = { \cfrac{hf}{c} } \)

And for the photon, c=λf, so the above equation becomes:

\( {P} = { \cfrac{h}{λ} } \)

The wavelengths of the incident photon and the scattered photon are related to each other like the below:

$$ { λ_{scattered\;photon} - λ_{incident\;photon} } = \cfrac{h \times (1-cos(θ)) } {mc} $$

where h is Planck's constant (6.626x10^-34 joule-seconds), m is the electron's mass (9.11 x 10^-31 kilograms) and θ is the scattering angle of the photon (take a look at the figure-3)
So the difference in the wavelength between the scattered photon and the incident photon changes from zero if the photon continues on its way undeflected (θ=0°) to h/mc if the photon is scattered through 90° (θ=90°).
The quantity h/mc appears frequently in the Compton Scattering, so it is call the "Compton Wavelength":

\( λ_{Compton}= { \cfrac{h}{mc} } \) which is equal to 2.43 x 10^-12 meters.
If we substitue the Compton Wavelength in the formula for Compton scattering ( Equation(1) ), it changes to :

\( { λ_{scattered\;photon} - λ_{incident\;photon} } = λ_{incident\;photon} \times (1-cos(θ)) \)

So even though the photoelectric effect was explained by Einstein using the particle nature of that light , It is the Compton Scattering experiment that proved the particle nature of the light which has put any doubts regarding the issue to rest.