Deducing The Equations For The Discrete Energy Levels And Radii Of Electrons In The Atoms
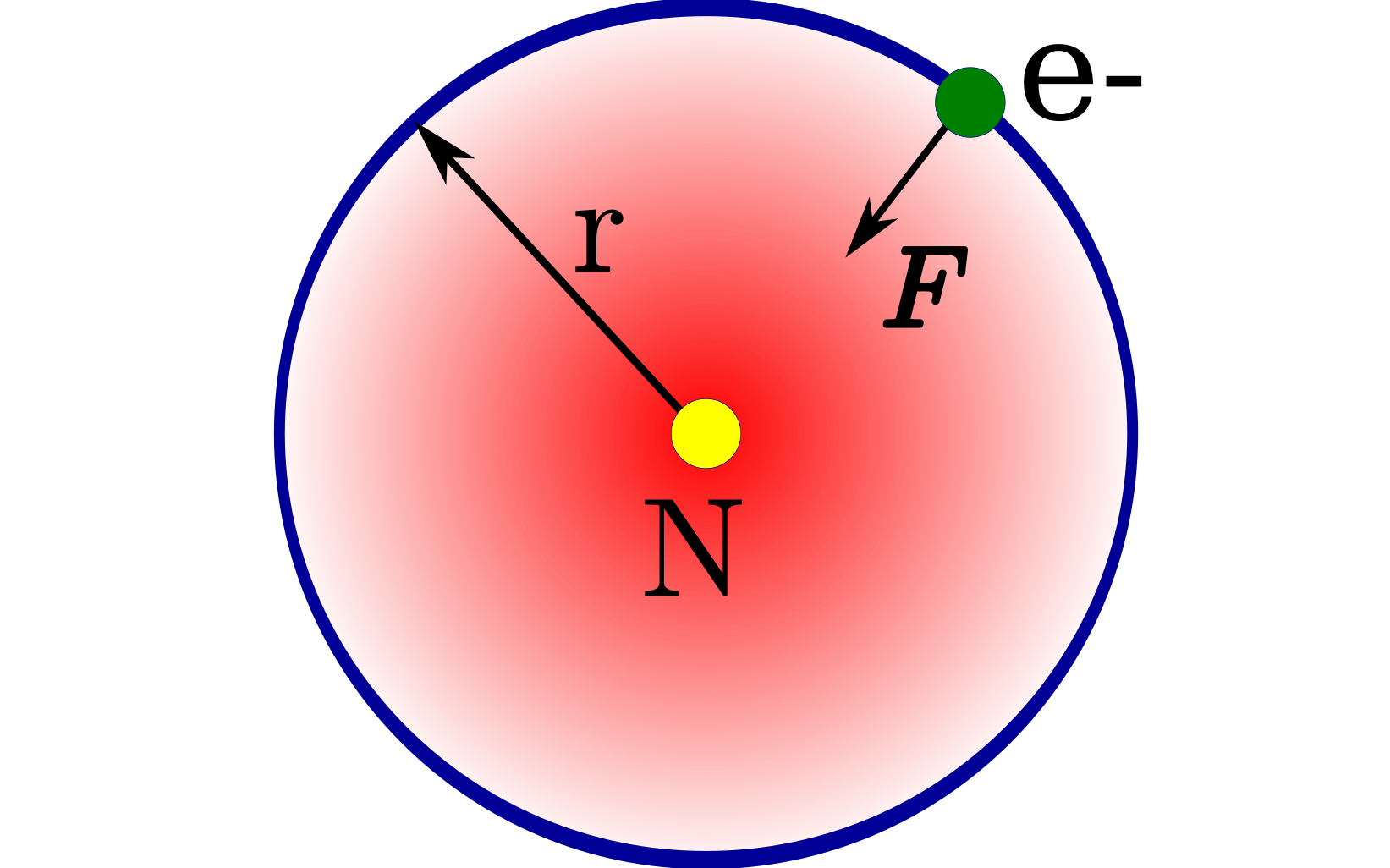
Image credit: Wikimedia Commons, Image Source
Niels Bohr took to the task of explaining the observed line spectra of one-electron atoms like H,He+,Li2+. He devised a new model for the Hydrozen atom. Combining the new ideas of Max Planck and Albert Einstein, he hypothesized the new model of the atom. He proposed that electrons can exist only with certain energy levels (or degrees) in the atoms. They can not have any random energy level. This idea is similar to the theories proposed for the quantization of black body radiation.
He suggested organizing the electrons only in specific orbits in an atom. These orbits correlate with the total energy allowed for electrons including kinetic energy and electric potential energyy. The below picture depicts the Bohr model of the atom. This model is in accordance with the discovery made by Rutherford that the positive changes should be compacted together at the nucleus.
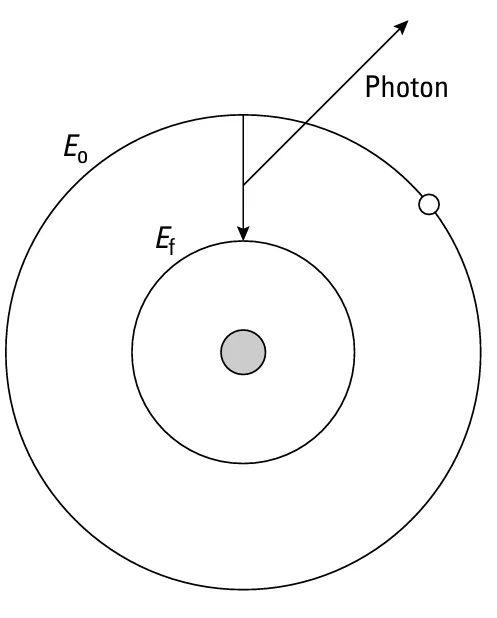
FIGURE-1: Bohr model of the atom
Moreover, Bohr incorporated the then new ideas of Einstein about photons and theorized that when electrons jump from a higher orbit (with more energy and a larger orbital radius) to a lower one (with less energy and smaller orbital radius), they emit a photon (electromagnetic radiation). The proposal that only certain orbits are allowed explains the specific wavelengths seen in the spectrum of gases.
To say it otherwise, when an electron jumps from a higher orbit where the total energy of the electron is Eo, to a lower one where the total energy of the electron is Ef , then the energy of the photon emitted by the electron hf is
where h is the Planck's constant 6.626x10-34 J-s and f is the frequency of photon.
This Bohr's model explained the observed atomic spectra successfully and got recognzied over the time.
Determining The Discrete Energies Of The Electrons In The Atom
An electron's kinetic and potential energy add up to its total energy.So
\( E = \cfrac{1}{2}mv^2 - \cfrac{kZe^2}{r} \)
where m is the mass of the electron,
v is its speed,
k is Coulomb's constant,
Z is the number of protons in the nucleus ,
e is the electron's charge,
r is the radius of the electron's orbit.
v is its speed,
k is Coulomb's constant,
Z is the number of protons in the nucleus ,
e is the electron's charge,
r is the radius of the electron's orbit.
\( F = \cfrac{kZe^2}{r^2} \)
And additionally, centripetal force equals
\( F = \cfrac{mv^2}{r} \)
You can equalize the two forces and resolve:
\( \cfrac{mv^2}{r} = \cfrac{kZe^2}{r^2} \)
\( mv^2 = \cfrac{kZe^2}{r} \)
When you enter this into the formula for total energy, you get:
\( E = \cfrac{1}{2} \cfrac{kZe^2}{r} - \cfrac{kZe^2}{r} \)
\( E = \cfrac{-kZe^2}{2r} \)
Determining The Permitted Electron Orbit Radii In The Atom
Without knowing the permitted values of the radius r, you can not do much with Bohr's equation for the energy of an electron in an atom . Bohr proposed the idea that atoms have quantized angular momentum, or the angular momentum of electrons.\( L = mvr \)
Bohr thus established the following correlation between this quantization and angular momentum:
\( L_{n} = mv_{n}r_{n} = \cfrac{nh}{2π} \;\;\;\;\;\;\;\; n=1,2,3... \)
n is an integer where the values of n correlate to the different permitted values of the angular momentum.
To put it another way, the angular momentum is a multiple of h/2p .
\( v_{n} = \cfrac{nh}{2πmr_{n}} \;\;\;\;\;\;\;\; n=1,2,3... \)
We are also aware that :
\( mv^2 = \cfrac{kZe^2}{r} \)
Calculating the speed squared provides you with
\( v_{n}^2 = \cfrac{n^2h^2}{4π^2m^2r_{n}^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
And
\( mv_{n}^2 = \cfrac{n^2h^2}{4π^2mr_{n}^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
Consequently, we can adjust the two mv2 numbers to equal one another:
\( \cfrac{kZe^2}{r_{n}} = \cfrac{n^2h^2}{4π^2mr_{n}^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
When you solve for rn, you get:
\( r_{n} = \cfrac{h^2}{4π^2mke^2} \cfrac{n^2}{Z} \;\;\;\;\;\;\;\; n=1,2,3... \)
The permitted Bohr radii are as follows:
Finally, you may compute the permitted energies using this information.
The permitted Bohr radii in meters are shown here:
\( r_{n} = (5.29 \times 10^{-11}m) \cfrac{n^2}{Z} \;\;\;\;\;\;\;\; n=1,2,3... \)
Using the Bohr radius to determine the permitted energy for hydrogen
Go back and find the permitted energy levels . As you are aware of :Consequently, replacing r gives you
\( E_{n} = \cfrac{-2π^2mk^2e^4}{h^2} \cfrac{Z^2}{n^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
This is how it appears in joules:
\( E_{n} = (-2.16 \times 10^{-18}) \cfrac{Z^2}{n^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
And this is an illustration of the permitted energy levels in electron volts.
\( E_{n} = (-13.6) \cfrac{Z^2}{n^2} \;\;\;\;\;\;\;\; n=1,2,3... \)
What is the lowest energy an electron in hydrogen can have for instance? That would occur when Z (the atom's proton count) = 1 and n = 1, giving you the following:
\( E_{1} = (-13.6) (\cfrac{1^2}{1^2}) \;\;\;\;\;\;\;\; Hydrozen \; n=1 \)
\( = -13.6 \; eV \)
Thus, -13.6 electron-volts is the strongest an electron can be bound in hydrogen. In other words, one electron in the n = 1 state, also known as the ground state, requires 13.6 electron-volts of energy to liberate.
What about the hydrogen state with n = 2 ? The energy of this level appears as follows:
\( = -3.4 \; eV \)
Therefore, in the n = 2 state of hydrogen, an electron is bonded with an energy of -3.4 electron-volts. As you can see, the energy levels of the progressively higher states drop until the bound state energy reaches zero, indicating that the electron is completely unbound.
Calculating The Permitted Energy Levels For Lithium Ions Li2+
Here is something to be aware of: Only atoms with a single electron are addressed by the Bohr model. This is due to the fact that the model is still quite basic and ignores how electrons interact with one another, which influences the total energy of each electron. As every electron repels every other one, their overall energy is impacted.Hence, you can only use the equation for the energy levels if you have doubly ionized lithium, or a lithium atom with two electrons removed and only one remaining (such lithium ions have a net positive charge of +2), if you wish to apply the Bohr model to, say, lithium, which has three protons in its nucleus (Z = 3). The ground state energy of doubly ionized lithium is
\( E_{1} = (-13.6) (\cfrac{3^2}{1^2}) \;\;\;\;\;\;\;\; Lithium \; n=1 \)
\( \;\;\;\;\; = 122 \; eV \)
\( \;\;\;\;\; = 122 \; eV \)
Thus, the energy of doubly ionized lithium in its ground state is 122 electron-volts.
