Schrödinger Equation Derivation & Its Significance

The classical wave equation is:

\( y(x,t) = A cos(kx-ωt) \)

The above equation represents a simple progressive wave which is travelling towards the right where A is the amplitude, \( k (the \;wave \;number) = \cfrac{2π}{λ} \), and angular frequency \( ω = 2πf \) where \( f \) is the frequency of the oscillation of the wave, \(x\) is the displacement, \(t\) is the time.

This displacement function is equivalent to the general wave equation:

\( \cfrac{∂^2y(x,t)}{∂x^2} = \cfrac{1}{v^2} \cfrac{∂^2y(x,t)}{∂t^2} \qquad \qquad \qquad (1) \)

We can confirm that the cosine wave function is the solution to the above wave equation by substituting the corresponding partial derivate values.

\( \cfrac{∂y(x,t)}{∂x} = -kA sin(kx-ωt) \)

\( \cfrac{∂^2y(x,t)}{∂x^2} = -k^2 A cos(kx-ωt) = -k^2y \qquad \qquad \qquad (2) \)

\( \cfrac{∂y(x,t)}{∂t} = +ωA sin(kx-ωt) \)

\( \cfrac{∂^2y(x,t)}{∂t^2} = -ω^2 A cos(kx-ωt) = -ω^2y \qquad \qquad \qquad (3) \)

when we substitute the equations (2) , (3) into equation (1), we get : \( k^2y = \cfrac{1}{v^2} ω^2y \)

\( k^2 = \cfrac{1}{v^2} ω^2 \)

\( k = \cfrac{1}{v} ω \)

If we substitute \( ω = 2πf \) and \( k = \cfrac{2π}{λ}\) into the above equation



\( \cfrac{2π}{λ} = \cfrac{1}{v} 2πf \)

\( \require{enclose} \) \( \cfrac{\enclose{updiagonalstrike}{2π}}{λ} = \cfrac{1}{v} \enclose{updiagonalstrike}{2π}f \)

\( v=λf \qquad (4)\)

Equation(4) is the famous velocity formula from quantum physics relating the frequency \(f\) and the wavelength \(λ\) So it shows that the wave function is indeed the solution for the wave equation.

Now coming to the quantum mechanical wave function, let us make some plausible assumptions:

1. It must be consistent with the below De broglie-Einstein postulates: \( λ = \cfrac{h}{p} \qquad f = \cfrac{E}{h} \)
2. It must be consistent with the total energy equation for a particle :
   E = K.E + P.E
   \( K.E = \cfrac{1}{2}mv^2 = \cfrac{p^2}{2m} \)
   P.E = V(x,t)
   Force is nothing but the partial derivative of the potential energy: \( F = - \cfrac{∂V}{∂x} \)
   So the total energy can be written as : \( E = \cfrac{p^2}{2m} + V \)


3. The wave equation must be linear in the wave funtion \( ψ(x,t) \)
   That means if \( ψ_{1}(x,t) \) and \( ψ_{2}(x,t) \) are two different solutions, then any arbitrary linear combination of them will be a solution to the wave equation.
   \( ψ(x,t) = c_{1}ψ_{1}(x,t) + c_{2}ψ_{2}(x,t) \)
   This linearity of the wave functions ensures that we can add together waves to produce constructive or destructive interference patterns.


4. For a constant potential, the proposed differential equation will have sinusoidal traveling wave solutions of constant wavelength and frequency.
   That means if \( V(x,t) = constant → F = - \cfrac{∂V(x,t)}{∂x} = 0 →\) that means momentum p is constant as \( F =\cfrac{dp}{dt} → \) that means λ and f are constant.

So from the above total energy equation :

E = K.E + P.E = \( \cfrac{p^2}{2m} + V = \cfrac{h^2}{2mλ^2} + V(x,t) = hf \)

→ \( \cfrac{h^2 \times 2π \times 2π}{2π \times 2π\times 2mλ^2} + V(x,t) = \cfrac{h}{2π} \times 2πf \)

→ \( (\cfrac{h^2}{2π \times 2π} ) (\cfrac{2π \times 2π}{λ^2} ) \times \cfrac{1}{2m} + V(x,t) = (\cfrac{h}{2π}) \times 2πf \)

→ \( \cfrac{ħ^2 k^2} {2m} + V(x,t) = ħω \qquad \qquad \qquad (5) \)
where \( ħ=\cfrac{h}{2π} , k=\cfrac{2π}{λ} , ω=2πf \)

At first, let us assume the wave function to be \( ψ(x,t) = cos(kx-ωt) \)

When we differentiate this wave function twice with respect to x, we get the below equation:



When we differentiate this wave function with respect to t, we get the below equation:



Equation (6) contains the \( k^2 \) term and equation (7) contains \( ω \) term and comparing these terms to equation (5) , it implies that the wave equation should contain the second order partial derivate with respect to \( x \) and a first order derivative with respect to \( t \) .

So applying linearity principle, we can say that the total energy equation for the wave function is :

\( α \cfrac{∂^2ψ(x,t)}{∂x^2} + V(x,t) ψ(x,t) = β\cfrac{∂ψ(x,t)}{∂t} \qquad \qquad \qquad \color{blue}{(8)} \)

Let us fix the constants α and β

Let us assume \( ψ(x,t) = cos(kx-ωt)\) (which is borrowed from classical physics) and for a freely moving particle, potential energy \( V(x,t) = V_{0} \) is a constant value.

If we substitute the values of \( \cfrac{∂^2ψ(x,t)}{∂x^2} \) and \( \cfrac{∂ψ(x,t)}{∂t} \) into the above equation , then we get :

\( -αk^2 cos(kx-ωt)+V_{0} cos(kx-ωt) = β ω sin(kx-ωt) \)

which we can write in the following form:

\( (αk^2-V_{0}) cos(kx-ωt)+ β ω sin(kx-ωt) = 0 \)

In order to satisfy the above equation , it requires that \( (αk^2-V_{0}) = 0 \) and \( β=0 \)

So \( k^2=\cfrac{V_{0}}{α} \) and \( β=0 \) and it does not satisfy the equation (5)

So the wave function \( ψ(x,t) = cos(kx-ωt)\) borrowed from classical physics is not satisfying the equation (5).

So let us consider a more generic equation which involves \( cos\) and \( sin \) terms.

Let us say \( ψ(x,t) = cos(kx-ωt) + γ \; sin(kx-ωt) \)

If we differentiate the above function with respect to x, we get

\( \cfrac{∂^2ψ(x,t)}{∂x^2} = - k^2 \; cos(kx-ωt) - k^2 γ \; sin(kx-ωt) \)

If we differentiate the above function twice with respect to t, we get

\( \cfrac{∂ψ(x,t)}{∂t} = ω\; sin(kx-ωt) - ω\; γ\; cos(kx-ωt) \)

if we substitute these values into the equation (8), we get :

\( -αk^2 \; cos(kx-ωt) - αk^2 γ \; sin(kx-ωt) + V_{0} cos(kx-ωt) + + V_{0} γ sin(kx-ωt) = β ω \; sin(kx-ωt) - βωγ\; cos(kx-ωt) \)

If we rearrange this equation , we get :

\( -αk^2 [ cos(kx-ωt) + γ \; sin(kx-ωt) ] + V_{0} [cos(kx-ωt) + γ sin(kx-ωt)] = \cfrac{β ω}{γ} [ -γ^2 cos(kx-ωt) + γ\; sin(kx-ωt)] \)

if we take \( γ = +i \) where \( i \) is the imaginary number \( i = \sqrt{-1} \) and \( γ^2 = -1 \)

\( -αk^2 \enclose{updiagonalstrike}{[ cos(kx-ωt) + γ \; sin(kx-ωt) ]} + V_{0} \enclose{updiagonalstrike}{[cos(kx-ωt) + γ sin(kx-ωt)]} = \cfrac{β ω}{γ} \enclose{updiagonalstrike}{[ -γ^2 cos(kx-ωt) + γ\; sin(kx-ωt)]} \)

So we get :

\( -αk^2 + V_{0} = \cfrac{β ω}{γ} \) , compare it with equation (5) : \( \cfrac{ħ^2 k^2} {2m} + V_{0} = ħω \)

\( α = -\cfrac{ħ^2}{2m} \) and \( β = γħ = iħ \)

\( -\cfrac{ħ^2}{2m} \cfrac{∂^2ψ(x,t)}{∂x^2} + V(x,t) ψ(x,t) = iħ\cfrac{∂ψ(x,t)}{∂t} \qquad \qquad \qquad \color{blue}{(9)} \)

This equation (9) satisfy all the assumptions taken for quantum mechanical wave function and thus is the Schrödinger Equation

So the wave function \( ψ(x,t) = cos(kx-ωt) + γ \; sin(kx-ωt) \)
where \( γ=i \) , it becomes : \( ψ(x,t) = cos(kx-ωt) + i\;sin(kx-ωt) \)
which is a complex function and is the wave function in the Schrödinger Equation.

The significance of the schrödinger equation is that it determines the path of the electron wave over time in an atom. For example the electron orbitals within the hydrozen atom are the result of the Schrödinger equation.

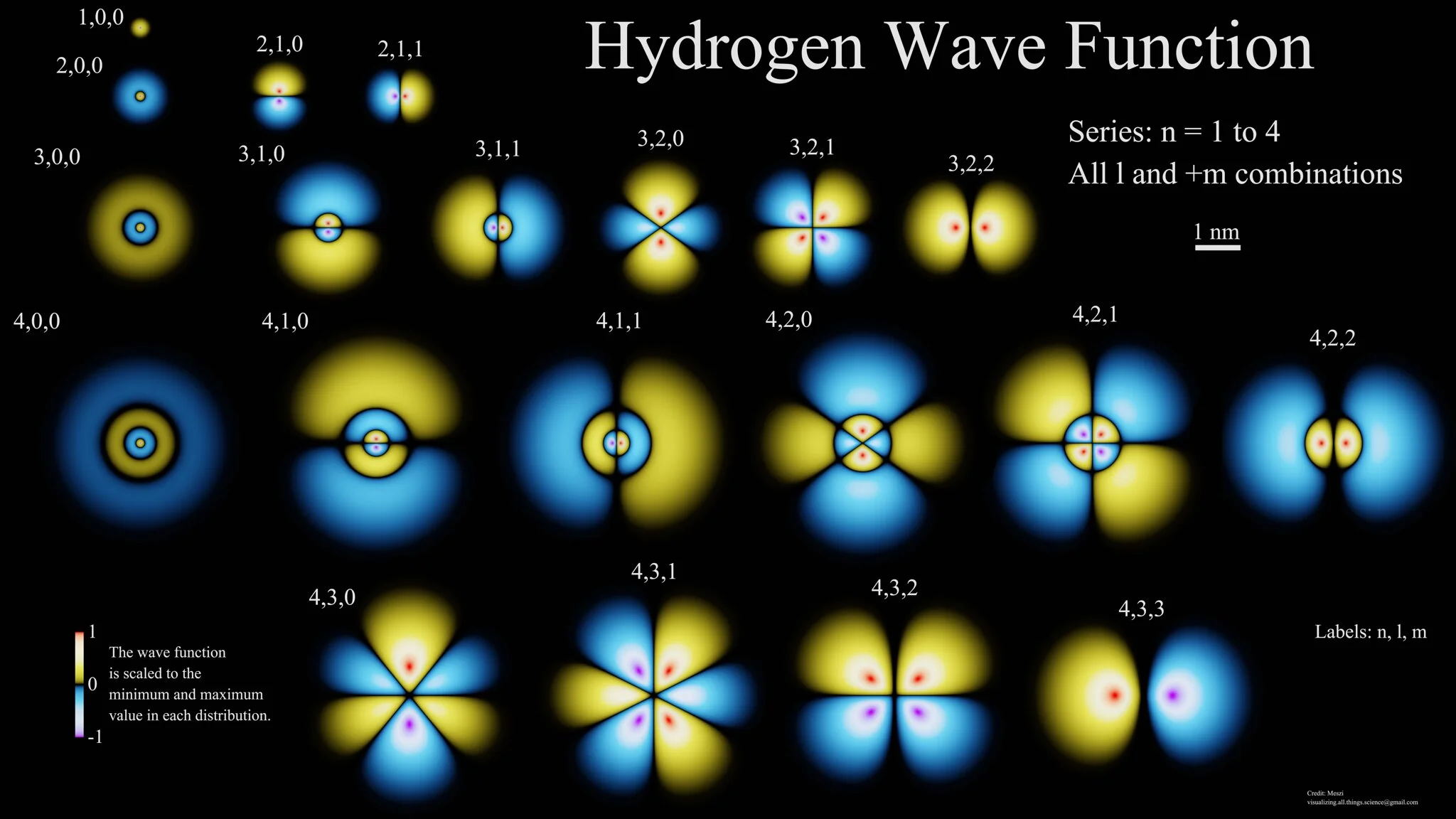
Image credit: flickr.com , Image source

The wave functions of hydrogen are displayed in this graphic when the principal quantum number, N, ranges from 1 to 4. The wave function, which characterizes the electron in its wave form, is the result of solving the Schrödinger equation. Blue and purple indicate negative numbers, whereas yellow and red indicate positive ones. When measured, the probability density-its complex square-actually indicates the potential location of the electron in the atom.