Cosmic "Dark Flows" - Mass Density Distribution Across The Universe
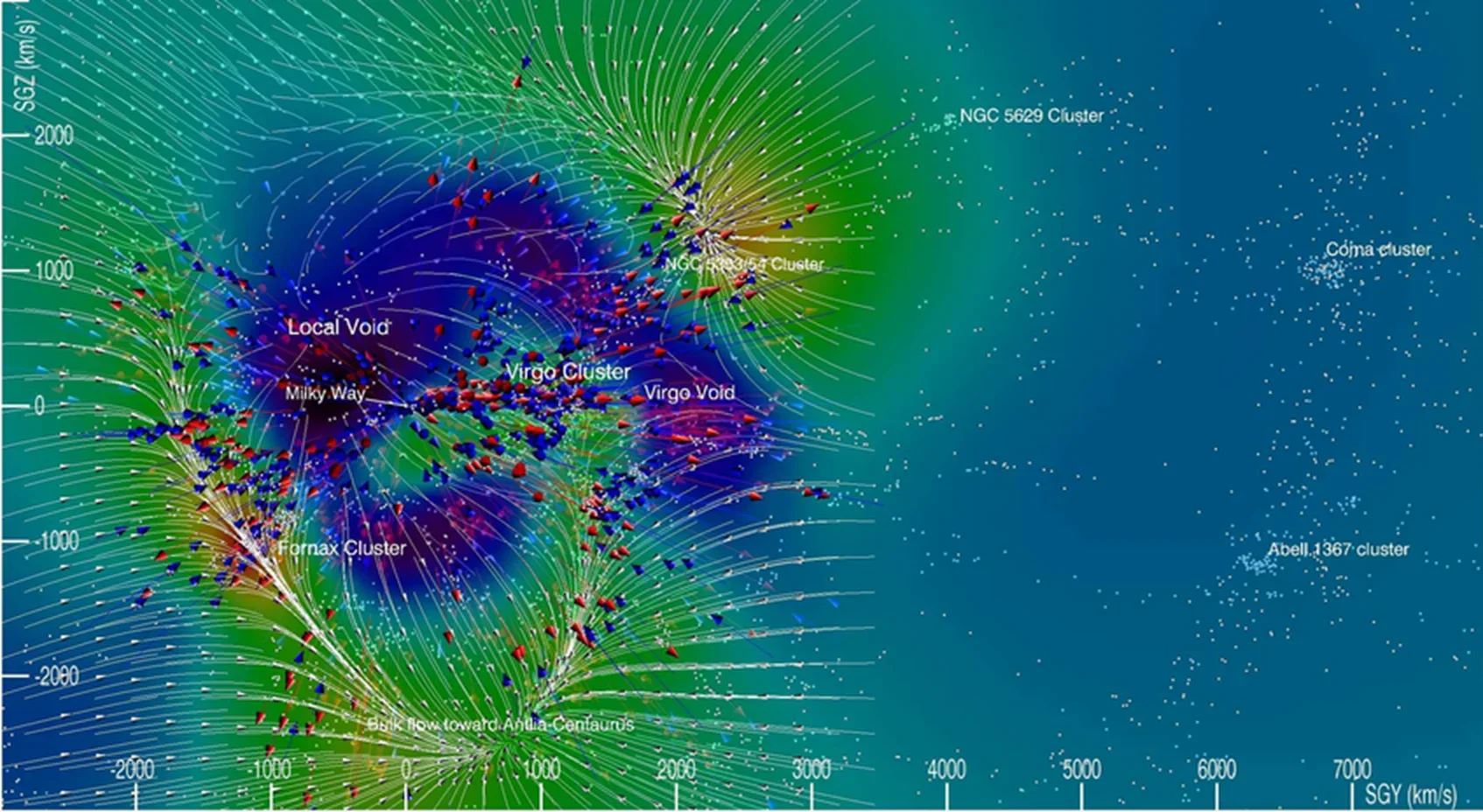
Physicists came to know that they can not do the authentic tracing of the true density of matter in the Universe using only the galaxy maps generated by redshift surveys because matter did not accumulate enough at all regions to form galaxies to glow and be visible. So matter that has not aggregated enough to form galaxies may still exist today but is not visible. That is the reason why redshift maps are not sufficient to trace out the density of matter in the Universe.
Any matter whether that is visible or not exerts gravity on the surroundings. So this gravity of all matter creates cosmic flows which allows for estimating the density of matter in the Universe. As galaxies blow off out of the cosmic voids and gather together into clusters and superclusters, they create irregularties in the expansion of the Universe and these irregularities are nothing but the "cosmic flows"
Physicists can use the surveys of cosmic flows to determine the distribution of the mass density in the Universe, along with any "dark matter" in between the galaxies.
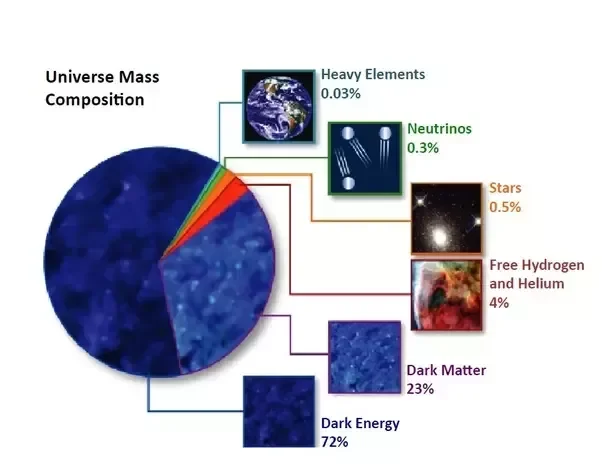
Image credit: NASA
Cosmic flows can estimate and chart up the clumping of matter even upto very large extents, they are the best reference points for determining the perfect or correct level of density dissimilarities in the Universe today. These reference points can aptly be compared against the CMBR (Cosmic Microwave Background Radiation) density dissimilarities across larger regions at earlier times. The velocities of the cosmic flows have roughly the same magnitude that is expected when COBE (Cosmic Background Explorer) measurements are taken into account by the standard dark-matter theories. These velocities are measured at a distance of 250 million light-years close to the Earth. This local consonance between the measured and predicated velocities of the cosmic flows shows that our fundamental theory of structure formation lasting for several decades is nearly right when the details on the nature of the dark matter are taken into account.
It is possible to approximate the total magnitude of matter in each galaxy by measuring the magnitue of the motions of the cosmic flows around specific clusters of galaxies. Regardless of whether the galaxies trace out the matter distribution or not, as long as they are measured in a consistent and correct way, physicists can generalize from the galaxy masses to come up with the total density of matter in the Universe. In other words, physicists can "weigh the Universe" and compute the most-sought-after parameter Ω which is nothing but the ratio of the mean mass density to the one needed for closing the Universe and finally halting its expansion for ever.
Mass Critical Density
The Universe has been expanding since its birth but its expansion is slowed down by the gravity. If enough matter accumulates in the Universe, then it can clog down the expansion and the Universe will implode onto itself in future. The density of matter that is just "sufficient" to stop the expansion of the Universe is called the "critical density".Deriving The Equation For Critical Density
Derivation of the critical density has to do with application of some basic physics concepts and Hubble's law.→ The formula for a system's kinetic energy, or motion energy, is : \( \cfrac{1}{2} mv^2\)
→ A two-body gravitating system's gravitational potential energy, or potential energy resulting from gravitational force, is expressed as: \( \cfrac{GMm}{r} \)
→ Hubble's law v=Hor says that in the universal spacetime, the relative recessional velocity v between two objects is exactly proportional to the separation between them r , where the constant of proportionality is Ho , the Hubble constant.
We derive the equation for critical density using the above three equations.
thus, specifying individually all the equations that we have:
Gravitational Potential Energy (GPE): \( \cfrac{GMm}{r} \)
Hubble's law \( v = Hr \)
Step1
K.E= |G.P.E|
\( \cfrac{1}{2} mv^2\) = \( \cfrac{GMm}{r} \)
\( v = {\sqrt { \cfrac{2GM}{r}}} \)
Step2
\( V = {\cfrac{4}{3} πr^3} \)
\( M = {ρ \times \cfrac{4}{3} πr^3} \)
\( v = {\sqrt { \cfrac{2Gρ4πr^3}{3r}}} \)
\( v = {\sqrt { \cfrac{8πGρr^2}{3}}} \)
\( (Hr)^2 = { \cfrac{8πGρr^2}{3}} \)
\( (H)^2 = { \cfrac{8πGρ}{3}} \)
\( ρ = { \cfrac{3H^2}{8πG}} \)
Calculating The ρcrit
ρcrit = \( 3H_{o}^2 \over 8πG \)
We can calculate the critical density ρcrit as below:
The Gravitational Constant G = 6.67 x 10-11 Nm2/kg2
Hubble Constant Ho=65 km/s/Mpc.
Let us first convert the Hubble constant to meters/second: Ho = \( {65 \times 1000} \over (3.1 \times 10^{22}) \) = \( {2.1 \times 10^{-18}} s^{-1} \)
Now we can solve for critical density:
ρcrit = \( { 3 \times (2.1 \times 10^{-18})^2 } \over {( 8 \times 3.14 \times 6.7 \times 10^{-11} )}\) = 7.9 x 10-27 kg/m3 ≈ 10-26 kg/m3
This ridiculously low density is equal to around 5 hydrozen atoms per cubic meter. However, in that same cubic meter, there exists microwave background radiation of 5 to 10 billions of low-energy photons which is the feeble antique remnant of the big bang.
How effectively does this density measure up to the density of bigger objects in the universe? Commonly there is a distance of about 2 Mpc between large galaxies, so we can verify what the average density is going to be if we consider that there is a square box that is 2 Mpc across and a galaxy such as the Milky Way is the only single object in it .
The volume of a 2 Mpc cube is ⇒ \( \left(2 \times 3.1 \times 10^{22}\right)^3 = 2.4 \times 10^{68} m^3.\)
Therefore the typical density is = mass divided by volume = \( 2 \times 10^{42} \over 2.4 \times 10^{68} \) ≈ \(10^{-26} \cfrac{kg}{m^3}\) .
So from the above calculations, It can be seen that the density at which the galaxies are spread out in the space matches up to nearly the critical density.
e The density parameter Ωo is the ratio of the observed density to the critical density:
The density parameter is just a number that does not have any units. There are three possible scenarios:
→ If ρ > ρcrit, then the value of Ωo > 1 - then the universe is closed and it will eventually collapse.
→ If ρ < ρcrit, then the value of Ωo < 1 - then the universe is open and it will expand forever.
→ If ρ = ρcrit, then the value of Ωo = 1 - then it represents a flat universe which will expand forever at an ever-decreasing rate.
In what proportion is the actual measurements of matter density to the critical density? Mass measurements from the largest surveys show that Ωo = 0.2 to 0.3, or a few tenths of the critical density. However, most of this mass exists as dark matter! The density of normal matter is in fact 5 times lower, leading to Ωo = 0.04 to 0.05. So if the critical density indicates five hydrogen atoms per cubic meter, our universe consists of only one hydrogen atom per 4 to 5 cubic meters. The density can be comparted to a single hydrogen atom in a volume of the size of a small bathroom. The rest of the mass is composed of pervasive dark matter - physicists do not know yet what type of particles they are.
How does the CMBR (cosmic background radiation) in the universe correspond to calculations of critical density? Physicists observed that the CMBR consists of 109 photons per cubic meter. It means that micrwave photons outnumber hydrogen atoms by ten billion times in the universe. We can compute the corresponding mass of all this CMBR radiation applying the formula E = mc2. The result indicates that all the microwave photons in the space are tantamount to 5 x 10-31 kg/m3, a density that is 20,000 times lower than the critical density. In other words, the density parameter from big bang radiation contributes only 1/20,000 = 0.00005, which is much lower than the density parameter contributed by matter. In spite of the huge number of microwave photons, matter is still most abundant in the Universe.
