Evidence For Dark Matter - Curvature Of Spiral Galaxies Rotation & Application Of Virial Proposition

Image credit: NASA , Image source

Most of the evidence for dark matter is gravitational , which means it can be detected only through its gravitation effects on the surrounding objects. The divergence between the lucent matter and the matter exerting the gravitational force gives an evidence for the existence of a enormous undetected (invisible) mass in the Universe.

When physicists need to estimate the gravitational mass of a galaxy or of a galaxy cluster , they analyze the movement (motion) of a galaxy and apply the gravitational computations to approximate the gravitational mass needed to keep the system confined, similarly to the way that the gravitational attraction between the Sun and the Earth equilibrates the movement (motion) of the Sun and the Earth about the Sun.

In case of a galaxy, what is commonly gauged is the movement of the stars. The stars in a galaxy rotate around the center nucleus of the galaxy. Though ordinarily , their orbiting paths around the galactic center are more or less circular but in fact, they coggle about their closed bound pathways because of the gravitational effect of the other surrounding objects. So they have a backward and forward movement along the radial position and show the other crosswise movements vertical to the radial position. Surveys of the radial movement are fundamentally carried out using the spectroscopic method in which the "red shifing" or "blue shifting" of the visible light emitted by a star is computed commonly. When light source is moving towards the observer, light will shrink in wavelength because of the Doppler effect and so appear to have a shorter wavelength which is "blue shifted". In the other case, when the light source is moving away from the observer, light will stretch out in wavelength and appear to have a longer wavelength which is "red shifted". Mensurating the crosswise motion of the star is more wearisome and difficult but with these motions considered together, it is possible to estimate the true motion of the star with in the galactic space. Commonly, a star moves reasonably circularly in a spiral galaxy. So we can reckon that the centripetal force generated by the circular motion is exactly counterbalanced by the gravitational force of the galactic center on the star so as to continue it in circular motion.

Curvature Of Spiral Galaxies Rotation

The orbital velocities of the stars at different radial positions from the galactic center yield the rotational curve of a galaxy. So the rotational curve of a galaxy is the orbital velocities of the stars in that galaxy as a function of the radial position of the stars from the center of the galaxy. A spiral galaxy generally has a central extrusion at which most of the mass is condensed and the spiral arms strewed across a disk.

So the equation for the gravitational force balancing out the centrifugal force due to a star rotating around the center of a galaxy at a distance of \( r \) with an orbital velocity \(v_{r}\) is as follows:

$$ { m(v_{r})^2 \over r } = { GmM_{r} \over r^2 } $$ \( M_{r} \) is the mass contained inside the radius \(r\)

If the star is inside the compact central zone of the galaxy, then \( M_{r}= \cfrac{4}{3}πr^3ρ \) where ρ is the modal density in the central zone. So inside the central zone, it is expected from equation(1) that

\( v_{r} ∼ r \) (proportional to \( r \))

But when a star is orbiting outside this central zone, the mass \( M_{r} \) can be considered invariable. So from the equation (1), it follows that \( v_{r} ∼ \cfrac{1}{\sqrt{r}} \)

So from the above analysis, it follows that in case of a spiral galaxy, the fluctuation in the velocity \( v_{r} \) with \( r \) has to reflect an increase at first (when \( r \) ≲ the radius of the central zone) and then has to undergo a decline (Keplerian decline) according to \( \cfrac{1}{\sqrt{r}} \)

But the surveys conducted for measuring the rotational curves for many spiral galaxies show that \( v_{r} \) = constant as \( r \) increases.

Then it can be deduced from the equation (1) that \( M_{r} \) ∼ \( r \) which indicates that there should be a huge amount of undetectable mass in the galaxy. This invisible mass or dark matter is thought of as forming a "halo" which the galaxy is enclosed within. The below is the image of one such rotational curve which depicts the features mentioned above.


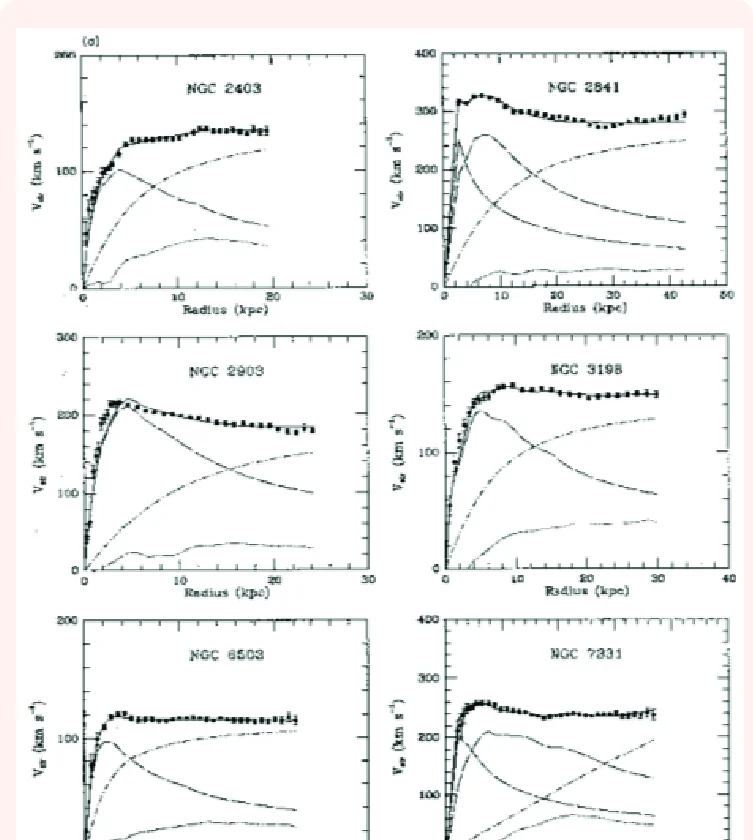
Spiral galaxy rotational curves, showing the contributions of gas (dotted), dark matter halo (dash-dot), and bright components (dashed). The data is represented by the square blocks. The solid line fits the dark matter concept. In 1991, Begeman et al.

Image credit: Sharma, Rakesh & Singh, Ksh. Newton & Aria, Anil. (2017). Signature of Dark Matter. Physics & Astronomy International Journal. 1. 00001. 10.15406/paij.2017.01.00001.
Image source

And the below is the schematic diagram of the dark halo surrounding the galaxy.



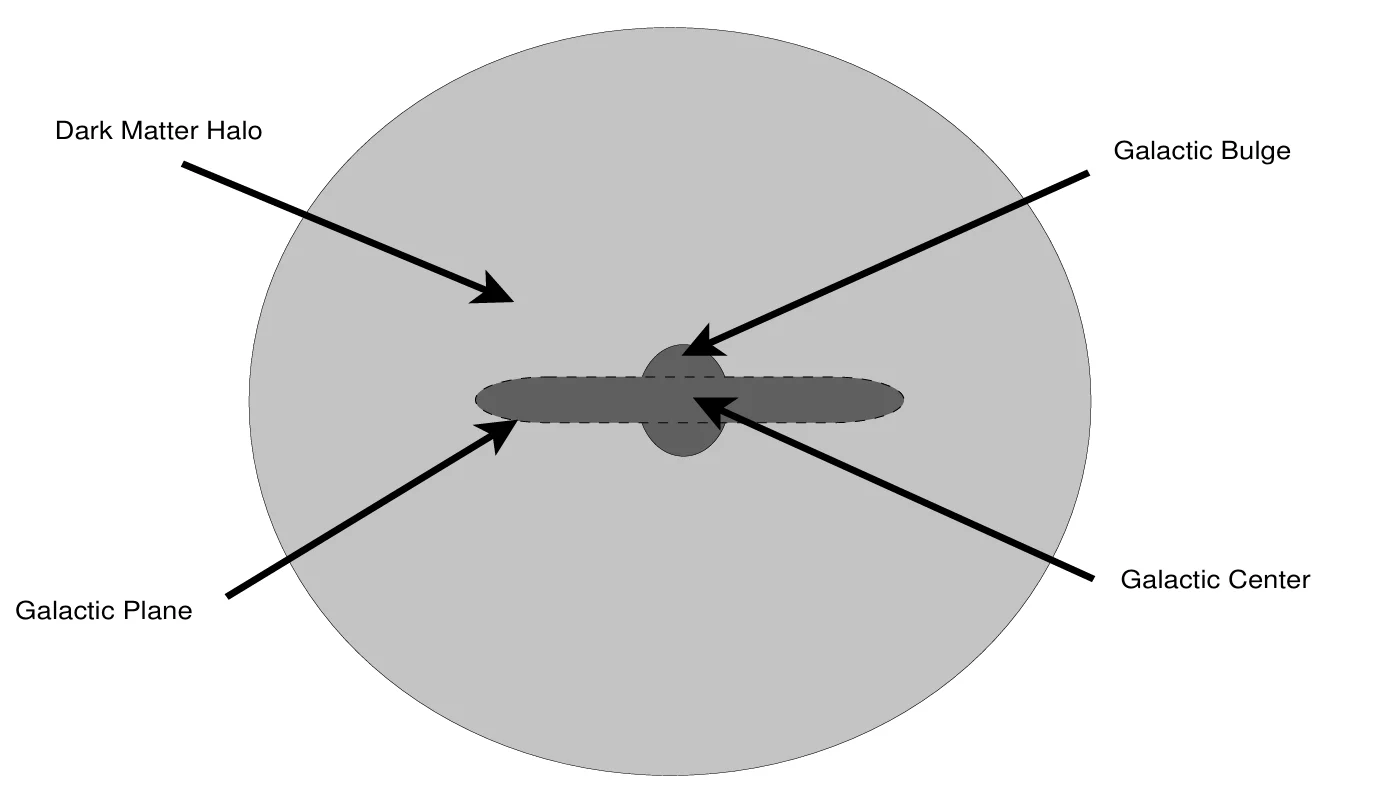
Diagrammatic representation of a disk galaxy contained within a dark matter halo, edge on.

Dark Matter In Galaxy Clusters

A galaxy cluster is a cumulation of a number of galaxies bound together by a gravitational force exerted commonly by the entire cluster. Generally, they are enclosed in a gas-dust emitting X-rays. Physicists derive the existence of dark matter in such a cluster generally by calculating its mass from their kinetics regulated by the gravitational influence of the system and analogizing them with the masses expected from their brightness level. Any surplusage of mass from the former calculation over the latter one suggests the existence of the dark matter in the cluster. The calculation of the dynamic mass is achieved using the virial theorem.

Virial Proposition

Let us say a body of particles are interacting with each other in non-relativistic way and are in a dynamic balance due to a centripetal force from their rotation around the center of the system. So it is a bound system. The virial proposition correlates the time-averaged kinetic energy to the time-averaged potential energy. Let us say the net force \( \vec{F_{i}} \) is being exerted on the \(i^{th} \) particle which has a position vector \( \vec{r_{i}} \) and a mass \( \vec{m_{i}} \), then the virial \( W \) of the system of \( n \) such particles is : $$ W = { \sum_{i=1}^n \vec{F_{i}}.\vec{r_{i}} } $$ since $$ \vec{F_{i}} = { m_{i} \cfrac{ {d^2\vec{r_{i}}} } { dt^2 }} $$ We can deduce from the equation (2) $$ W = { { m_{i} \cfrac{ {d^2\vec{r_{i}}} } { dt^2 }}.\vec{r_{i}} } $$ $$ = {\sum_{i=1}^n m_{i} \cfrac{d}{dt} (\dot{\vec{r_{i}}}.\vec{r_{i}})} - {\sum_{i=1}^n m_{i} (\dot{\vec{r_{i}}}.\dot{\vec{r_{i}}})} $$ The second term in the above equation represents double the total kinetic energy (translational) and the first term can be represented in terms of the moment of inertia \( I = m_{i}\vec{r_{i}}.\vec{r_{i}} \)

From the equation (5), the virial becomes (K indicating the kinetic energy):
$$ W = { \cfrac{1}{2} \sum_{i=1}^n \cfrac{d^2}{dt^2}(m_{i}\vec{r_{i}}.\vec{r_{i}}) - 2K }$$ $$ = { \cfrac{1}{2} \sum_{i=1}^n \cfrac{d^2}{dt^2}I - 2K }$$ When the system is in dynamic balance, the moment of inertia I would remain constant over time, so the first term in the equation (7) becomes zero, and the equation becomes: $$ W + 2K = 0 $$ The gravitational force of a self-gravitating system on the \( i^{th} \) particle of mass \( m_{i} \) from all other particles can be represented as : $$ F_{i}= { \sum_{j \neq i} Gm_{i}m_{j} \cfrac{( \vec{r_{j}} - \vec{r_{i}} )} {| \vec{r_{j}} - \vec{r_{i}} |^3} } $$ From equation (2), $$ W = { \sum_{i=1}^n \sum_{j \neq i} Gm_{i}m_{j} \cfrac{\dot{\vec{r_{i}}}.( \vec{r_{j}} - \vec{r_{i}} )} {| \vec{r_{j}} - \vec{r_{i}} |^3} } $$ $$ = -\cfrac{1}{2} \sum_{i=1}^n \sum_{j \neq i} G \cfrac{m_{i}m_{j}} {| \vec{r_{i}} - \vec{r_{j}} |} $$ = V (total gravitational potential energy )

Equation (8) can be represented as (using the annotation T for K): $$ V + 2T = 0 $$
We can compute the potential energy V of a self-gravitating sphere (like a galaxy cluster) of mass M (density ρ) and radius R as follows: \( V = - \int_0^R G \cfrac{(\cfrac{4}{3}πr^3ρ) (4πr^2ρ)}{r} dr \)

\( = - G \cfrac{R^5}{5} (\cfrac{4}{3}πρ) (4πρ) = - \cfrac{3}{5} G \cfrac{(\cfrac{4}{3}πR^3ρ) (\cfrac{4}{3}πR^3ρ)}{R} \)

$$ = - \cfrac{3}{5} \cfrac{GM^2}{R} $$ Such a cluster will have a total kinetic energy of \( T = \cfrac{1}{2}Mv_{rms}^2 \) where \( v_{rms} \) is the root mean square speed of each galaxy in the cluster.

We can estimate the gravitational mass \(M\) of such a self-gravitating system in a dynamic balance from equation (12) if we know the radius \(R\) and \(v_{rms}\) from the measurements.



Elliptical Galaxy M87
Image credit: NASA , Image source

Application Of Virial Proposition

The famous physicist Zwicky gauged the velocities of such galaxies in the Coma cluster and calculated the gravitational mass of the Coma cluster in 1933. Using the then known orbital velocities of seven galaxies in the Coma cluster , he calculated the root mean square velocity of each galaxy. Assuming that the Coma cluster has the usual shape of a sphere and the galaxies inside it are having the same mass, we can calculate the total kinetic energy as \( T = \cfrac{3}{2}Mv_{rms}^2 \) where \( M \) is the mass of the cluster and the gravitation potential energy is given in the equation (13).

He applied the equation (12) to calculate the gravitational mass \( M \) of the Coma cluster. He computed the mass-to-luminnosity ratio \( M \over L \) ( in the units of \( M_{⊙} \over L_{⊙} \) which is the mass-to-luminosity ratio of the Sun ) for the Coma cluster, using the then known luminosity from the visible light of the cluster and examined it against that of each galaxy. Having done that, he came to know that the calculated \( M \over L \) of the Coma cluster is almost 50 times more than that of any particular galaxy. This suggests an invisible mass in enormous amounts causing the gravitational effect in the Coma cluster. Recently, more advanced measurements are carried out for different \( M \over L \) ratios for both of the cluster and each particular galaxy. However the factor of 50 which was deduced by Zwicky has remained the same.

Sinclair Smith took up the task of calculating the luminosities ratios for the Virgo cluster, three years after the Zwicky's measurements. the Virgo cluster (see the below image) is in a good proximity to the cluster Local Group (in which Milky Way and Andromeda are situated) but it has an irregular shape.



The Great Virgo Cluster
Image credit: Wikimedia Commons , Image source

There are mostly elliptical galaxies and S0 type galaxies (flat spiral) in the cluster. In elliptical galaxies the movement of the individual stars along the radius is arbitrarily apportioned and so they can not produce a veritable rotational movement in the galaxies. So the elliptical galaxies are a spread out, arbitrary apportion of stars and gas-dust. This unpredictable arbitrary movement of the stars hanging out in an elliptical galaxy bears upon the combined average movement of such galaxies within a cluster such as the Virgo. The motions of the elliptical galaxies within the Virgo cluster are also unpredictable. This makes the Virgo cluster not adopt a veritable spherical shape , just as does the Coma cluster which the spiral galaxies preponderate. The approximations of gravitational mass and the brightness level of the Virgo cluster also corroborate the existence of undetectable dark matter haging out in the Virgo cluster.

It was later found out that the "perceptible" part of galaxy clusters like the Coma cluster comprises two components. One component incorporates the galaxies which give off light in the visible spectrum and the other component consists of the massive amount of gas giving off X-rays that interpenetrates through the galaxies diffusing in the cluster. The gases giving out the X-rays are heated up to a very higher degree of temperature(∼ 10⁶K) and are much more rugged when compared to the galactic matter in the cluster. The hot gas hanging out in the galaxy system are enkindled by the energy of the hot gas, galaxies and the dark matter. The hot gas which has been aroused to an extremely high temperature ∼ keV gives off X-rays. The brightness level of such a cluster is approximated by the visible galaxies and more significantly by the lambency of the hot gas that is examined through a X-ray telescope. Recent computations which were done using these obervations and better measurements of the movements of the galaxies also establish the existence of the dark matter hanging around in the galaxy cluster.