Gravitational Lensing - Crooking Of Light & The Phenomena Of The Lyman Alpha Forest

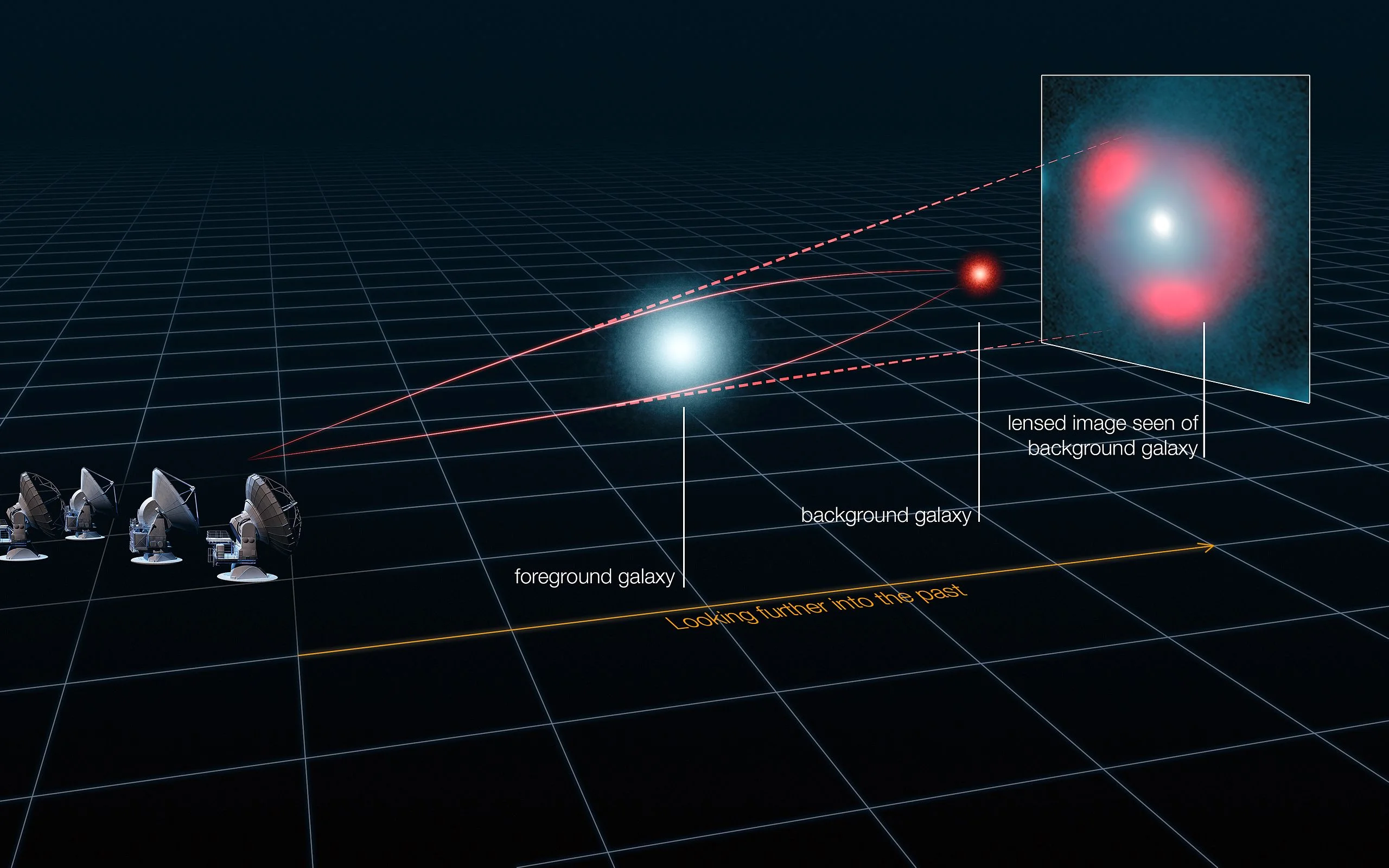
Image credit: Wikimedia Commons , Image source

The crooking of light when it is traveling through in the region of a gravitational mass brings about the lensing effect. This happening is called "gavitational lensing". It is a straightforward and candid effect of general theory of relativity put forth by Einstein which says that gravity governs the geometry of the space. Light travels in such a crooked path in the region of a gravitating body, resulting in the lensing effect. The beholder in the prospect of such a lensing mass may get to find or see twisted or quite a many images of an object that may exist in behind of the gravitating mass at a reasonable distance. The gravitating mass functions as a lens in this manner to the light being emitted from a background object.

Astronomers observed such lensing effects without any evident indication of lambent mass that can produce such lensing of the background objects. So it points at the existence of an enormous undetectable matter or dark matter.

The gravitational lensing effect and its evidence in the observational astronomy is generally categorized in three classes - that is to say - strong lensing, weak lensing and microlensing. The strong lensing gives rise to multiple images or Einstein's rings for a far-off object in the background. In case of a weak lensing, distorted or deformed images are produced for a background object. The gravitational microlensing causes the brightness of the object lying behind the gravitating mass to look as if it has spiked up , to a beholder in the foreground.

The gravity of a point mass with a magnitude of \( M \) produces deflection of a light ray at an angle which is given as : $$ α_{D}(x) = \cfrac{4GM}{xc^2} $$ Where G is the Newton's gravitational constant , \( c \) is the speed of light in vacuum and \( x \) is the nearest approacing distance of the light ray to the point mass. Factually, the light ray will pass being bent if the background object and the point mass producing the lensing effect are far away from each other, then the crooked path of the light can be estimated with two straight lines with the deflection angle refered to as \(α_{D}\). This estimation is called the "thin lens" estimation.

Using the space-time metric in the proximity of the lens as shown below , it is possible to obtain the above equation. $$ {ds^2} = { \left( 1+\cfrac{2φ}{c^2} \right) } c^2 dt^2 - { \left( 1-\cfrac{2φ}{c^2} \right) } dl^2 $$ In the above equation, it is assumed that the gravitational potential φ producing the lensing effect is tiny. Calculating the time taken (by applying the Fermat's principle) by the light photons to get to the beholder from the background object gives the correlation for the deflection angle \( α_{D}(\vec{x}) \) at the position \( \vec{x} \) as : $$ α_{D}(\vec{x}) = -\cfrac{2}{c^2} \int_{source}^{observer} ∇φdl $$ Where \( ∇ \) is the gradient vertical to the line of sight. So the above equation can be represented as : $$ α_{D}(\vec{x}) = \cfrac{4G}{c^2} \int d^2 x^{́} \int ρ(\vec{x}^́ r) \cfrac{\vec{x}-\vec{x}^́}{|\vec{x}-\vec{x}^́|^2} dr $$ Where \( ρ \) is the mass density of the lens and \( r \) is along the line of the sight direction. If we apply the "thin lens estimation" for a lens of point mass \( M \) , the above equation can be represented as the equation (1)

The equation (1) can be applied to lensing by an extended mass. In the specific case of mass distribution that is round-about symmetric, the crook angle \( α_{D} \) is given as : $$ α_{D}(R) = \cfrac{4GM_{R}}{Rc^2} $$ Where \( M_{R} \) is the mass embedded inside the radius \( R \) from the center of the lens.

The lens equation is the fundament to the calculation of the mass in a cluster through gravitational lensing. The lens equation correlates \( D_{S} \) which is the distance between the observer and the location of the source, to the deflection angle \( α_{D} \) and the distance \( D_{dS} \) between the source and the lens which is shown in the below image.


The geometry of gravitational lensing
Image credit: D. Dey, K. Bhattacharya and T. Sarkar, Phys. Rev. D 88, 083532 (2013), the American Physical Society. Image source
In the above image, \( S \) denotes the Source point, \( I \) the "Image" point and \( P \) is a point directly above the point marked "Lens" then the lens equation follows from the relation \( PI = PS + SI \) and is given by
$$ D_{S}θ = D_{S}β_{s} + D_{dS}α_{D} $$ Where θ and β sequentially are the angular positions of the image and the source with regard to the beholder and \( α_{D} \) is the crook angle. Defining a scaled crook angle α as $$ α = \cfrac{D_{dS}}{D_{S}}α_{D} $$ The lens equation in Eq (6) becomes: $$ θ = β_{s}+α $$ or $$ β_{s} = θ-α$$

For an orbitual mass apportionment , the above equation would not yield a singular solution but multiple solutions. It means that if an object is lensed by an orbitual mass apportionment , then there will be multiple images formed for this object.

Under the effect of intense gravitational lensing, arcs, rings or multiple images will be formed for the remote objects. If the lens, source and the beholder are perfectly aligned, then gravitational lensing will crank out ring images which are perfectly symmetrical. These rings are known as Einstein's rings. We can calculate the mass of the lens by applying the lens equation on the angular size of such a ring or arc. When it comes to weak lensing, the impairment of the image due to gravitational lensing is not completely so intense and the impairment of each image is scarcely identifiable. But if a lens cluster brings forth a lot of impaired images of remote galaxies , then the average impairment of the images can be investigated. So it means that the empirical measurements of impairments due to weak lensing have statistical nature.The remote dimmed galaxies (high red shift) can be thought of to be arbitrarily located. If they undergo weak lensing by a galaxy cluster (heavy mass concentration) and consequently show impairments along a specific direction (that means they are coherently patterned), then the exmination of such a coherent pattern plainly suggests weak gravitational lensing for the remote galaxies. Examining and probing into such a collection of impairments of images ( including their magnification), the gravitational field of the prospect cluster creating the lensing effect can be calculated which will in turn yield the profile of the matter density (including both baryonic matter and dark matter) or statistical mass apportion of the cluster. When the object lying in the background is well lined up with the lensing object lying the foreground, then the object in the background will appear more shining due to the gravitational lensing. If the object in the background and the lensing object locomote with respect to each other, the evident refulgence of the object in the background is fugacious to the beholder. A dim object also appears more luminous due to this physical effect of microlensing. We can perceive the microlensing effects by detecting the increase and decrease of luminosity of the source object as it locomotes with respect to the lensing object. So we can notice that the change in brightness over time (which is called "light curve") for such a moving object (which is moving with respect to the lensing object) will present an increase due to microlensing. The mass of the lens can be calculated from the examination of such light cuves.

Analysis On The Bullet Cluster - 1E0657-56

The galaxy cluster 1E 0657-56, also known as the "bullet cluster"
Image credit: NASA Image source
Physicists have put the strong and weak gravitational lensing effect to use to detect one of the most profuse attestations of the dark matter in the "Bullet cluster" which is otherwise called 1E0657-56. This cluster was brought about (produced) as a consequence of one of the most dynamical events that have occurred in the Universe after the Big Bang in which two gigantic galaxy clusters impinged on each other at a distnace of nearly 4 billion light years from the Earth in the constellation Carina. As a consequence of this impinging, the smaller cluster penetrated through the bigger one. Physicists used the X-ray analysis to make out the baryonic mass apportion of the two impinging clusters and the dark matter elements hanging around in them were rebuilt using the weak and strong gravitational lensing. This analysis demonstrated that after the impingement of the two clusters, when the smaller one interpenetrated through the core of the bigger one, the baryonic mass apportion of the smaller cluster underwent deformation in shape due to the severity of the collision and it assumed the shape of a bullet as a consequence of the collision. The analysis also demonstrated that the collision was so severe that it forced the baryonic matter (ordinary matter) in each clashing cluster to dislocate from its corresponding dark matter halo with the dark matter halos themselves having penetrated through each other rather unflustered and uncontorted. So in this way, the birthing of the bullet cluster not only shows an empirical proof of the presence of dark matter but also suggests that dark matter is more or less collisionless. Phsicists observed analogous results for the cluster MACS J0025.4-1222.

The Phenomena Of The LymanAlpha Forest

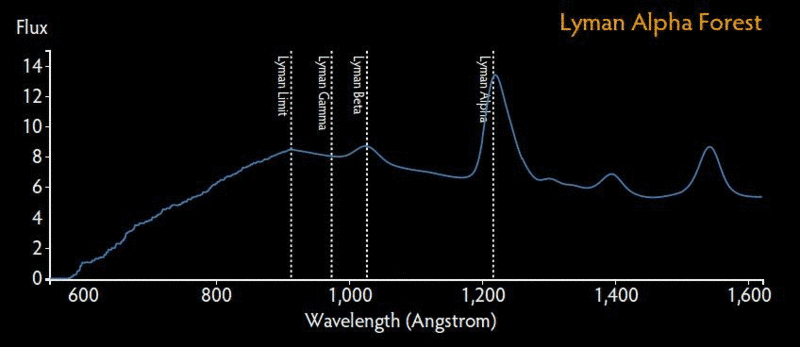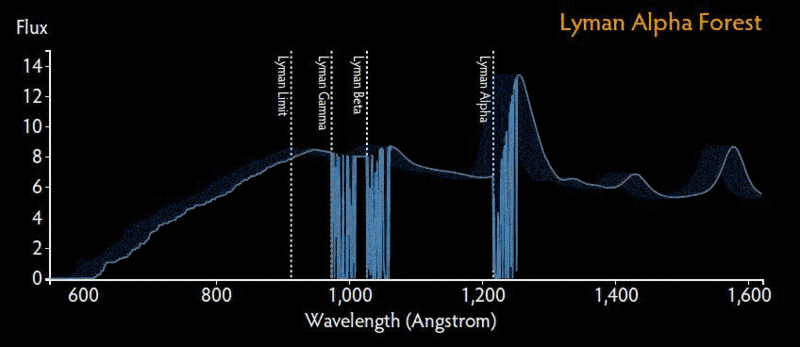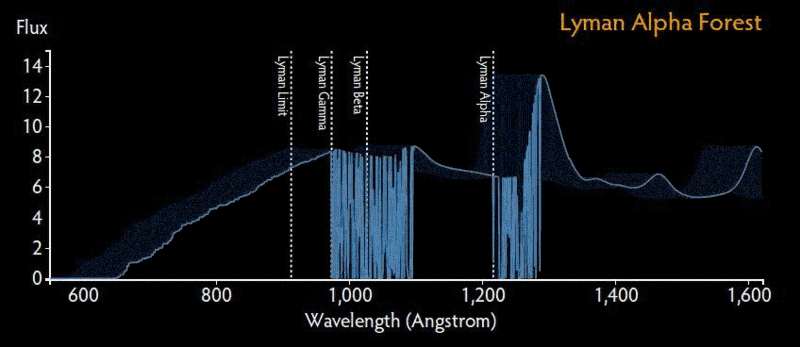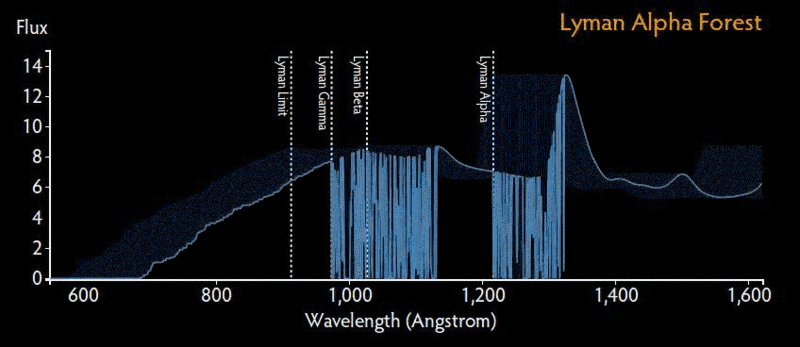
LymanAlpha Forest
Image credit: Wikimedia Commons Image source

When an electron in a hydrozen atom makes a transition from a higher orbit to the ground state (the lowest energy orbit) , it emits light in the form of photons whose energy is equal to the energy difference between the two oribits. These emission lines are called Lyman alpha lines. On the other hand, when a neutral hydrozen atom is impinged upon by a photon (electromagnetic radiation) which has sufficient energy, the electron transits from the ground state to a higher orbit. In this case, the energy that is equivalent to the energy difference between the two oribits will be absorbed by the electron and it will look like an absorption line to a viewer. Such sequences of absorption lines would then correspond to the energy series that would have been used up to raise the hydrozen atom in the ground state to a higher state in the intergalactic medium. This phenomena is called the "Lyman alpha forest"

This physical process of absorption occurrences which generates the Lyman alpha forest is detected in the absorption spectra of distant quasars which are also called quasi stellar objects (QSO). The photons (electromagnetic radiation) emitted from the quasars travel through the intergalactic medium which consists of hydrozen. When the neutral hydrozen atoms absorb the relevant energy from the photons, they generate the observed absorption spectrum of the Lyman alpha forest. The wavelength that is absorbed by a neutral hydrogen atom would have extended to a higher wavelength due to the Universe's expansion if it had made it all the way to the observer without being absorbed by the hydrogen atoms. So what would be visible to a distant observer (at Earth, for instance) is therefore, a Lyman alpha absorption line at a wavelength (extended) that matches the wave length at the moment and location of its absorption in the intergalactic gas of hydrogen. In this way, the Lyman alpha forest comprises information about the intergalactic medium or IGM.

The intergalactic medium contains gas that is impacted on by the gravitatinal potential of all the matter hanging around, including any dark matter that may possibly be present. Physicists used the Lyman alpha forest together with the computer simulations to find out that the interstellar gas makes up specific structures that are ordered in sheets and filaments which are called the "cosmic web" which agrees with the dark matter scenario indicating that the structures conform to the dark matter apportion at a large scale. The dark matter may confine the baryonic matter due to its gravitational collapse. According to the hypothesis of cold dark matter structure formation , there are a lot of cold dark matter halos with conglomerated interstellar gas surrounding them. But the masses of such halos are not sufficient to bring forth the stars and finally the galaxies. The heated gas pressure keeps the conglomerated gas from imploding any more creating a stable topology. If there are no stars that emit light, these types of structures can be detected only via the absorption spectra. So in this way, dark matter can also be examined via the Lyman alpha forest.